Clase2

• Retomando...
• Inicialización de la Población
• Función de Adaptación
• Mecanismo deSelección
• Renormalización de la Función de Adaptación
• Operadores Genéticos
• Operadores de Mutación
• Operadores de Cruce
• Parámetros de Control
• Algoritmo Genético Simple

Retomando...

La sesiónanterior concluyó con el planteamiento de la anatomía delos programas evolutivos. Allí tratamos un primer elemento esencialcomo lo es la representación genética de las soluciones(individuos, genotipos o cromosomas).

Destacamos que:

• La representación depende del problema considerado.
• Por lo general pararepresentar un cromosoma se utiliza una cadena de símbolos de longitudfija.
• Se sugiere que dichos símbolos pertenezcan a un alfabeto finito de la menor cardinalidad posible.
• La representación cromosómica más estudiada y empleada es la binaria.

 

Inicializaciónde la Población

Un segundoelemento importante de la anatomía de los programas evolutivos loconstituye la generación de la población inicial.

Por lo general,los programas evolutivos trabajan sobre una población de tamaño fijo, por ejemplo de n individuos. Lo usual es inicializarlosaleatoriamentecon una distribución uniforme sobre el espacio de configuraciones.Esto es, se generan n estructuras de datos aleatorias estadísticamente representativas de las potenciales soluciones del problema.

Es posible, aunque por lo general poco recomendable, el introducir en la poblacióninicial información sobre el problema. Esto sería una suertede combinación del paradigma creacionista con el evolucionista.
 

Funciónde Adaptación o Aptitud

Tambiénllamada función de aptitud, es una función que aplicadasobre un individuo produce como resultado uno o más números que miden la calidad del individuo como solución del problema en cuestión. Determina la conexión entre el programa evolutivo y el problema considerado.

Desde el punto de vista delaevolución natural la función de adaptación emulael ambientey es un factor esencial en el mecanismo de selección.

Importante: Dela adecuadaselección de la función de adaptacióndependeen muchola eficiencia y la eficacia del programa evolutivo.

En general no es relevantela forma cómo se evalúa esta función, lo cual permiteincorporar a ella la mayor cantidad de información posible. Porejemplo, en ciertos casos es posible incorporar en la función deadaptación lasrestricciones del problema.

En los programas evolutivos, por lo general el o los resultados de evaluar una función de adaptación se traducen en probabilidades para el mecanismo de selección. Recordemos que esta función mide la calidad de los individuos como soluciones al problema considerado y que para emular la selección natural setrata de escoger con mayor probabilidad a los individuos más aptospara que participen en la reproducción.

De aquí se desprenden dos hechos que conviene considerar:

• Es conveniente que la funciónde adaptación sea no negativa.
• A un mejor valor dela funciónde aptitud corresponderá una mayor probabilidad deselección.

Veamos algunos ejemplos de selección de la función de adaptación en un caso sencillo:

• Si el problema es maximizar la función y=sen(x) en el intervalo [0 ,180 ]se puede escoger como función de adaptación la misma función a maximizar y pues es no negativa y un mayor valor de y representaun individuo de mejor calidad.
• Si el problema es maximizar la función y=sen(x) en el intervalo [90,360]no conviene escoger como función de adaptaciónla misma funcióny ya que en cierta parte del dominiosehace negativa.
• Si se trata de minimizar lafunción y=sen(x) en el intervalo [0 ,180] no conviene escoger como función de adaptación la misma funcióna minimizar y pues un mayor valor de y no corresponde a unindividuo mejor adaptado. En este caso se podría escoger como adaptaciónuna función del tipo 1/(1+y) que cumple con lo requerido.

 

 

Mecanismo de Selección
 

Es un método que debe permitir escoger los individuos aptos para la reproducción, es decir, aquellos sobre los que se aplicarán los operadores genéticos.

En este proceso se debe dar más peso a los individuos más aptos sin que ello signifique despreciar por completo a los menos aptos. Obviamente el mecanismo de selección está ligado a la función de aptitud,que es la encargada de medir la calidad de los individuos.

A partirde lacuantificación de la calidad de los individuos se hace necesarioconstruir una distribución de probabilidades. El mecanismo deselección debe darle más posibilidad de participar en lareproducción a las estructuras más aptas. Existen muchas variantes de mecanismos de selección, pero el más común es el de rueda de ruleta.

Este mecanismo se puede describir como sigue:

1. Se hace quela funciónde adaptación sea positiva.
2. Se suman lasaptitudesde la población.
3. Se genera un númeroaleatorio uniformemente distribuido y se multiplica por la suma de aptitudesobtenida en el punto 2.
4. Se van sumandoparcialmentelas aptidudes de la población y se selecciona el individuoparael cual la suma acumulada sea mayor o igual al producto obtenido en 3.

Un ejemplo:

Supongamos quese tiene una población de 6 individuos cuyas aptitudes en la siguiente tabla:
 

Cromosoma número	1	2	3	4	5	6
Función deadaptación	100	90	80	70	60	50

 

Al hacerlas sumas parciales se tiene la tabla:
 

Cromosoma número	1	2	3	4	5	6
Función deadaptación	100	90	80	70	60	50
Suma parcial	100	190	270	340	400	450

 

Gráficamente, esta distribución de la adaptación puede verse como una torta de la forma:
 

 

Si al generar unnúmero aleatorio con una distribución uniforme se obtieneel valor 0.4, el producto 0.4x450 arroja el valor 180, por tanto se debeseleccionar el cromosoma número 2, ya que la distribución acumulada que éste presenta es 190. Gráficamente esta selección en la distribución acumulada puede verse como sigue:

Otros casosdeselección para este mismo ejemplo serían:
 

Número aleatorio	0.1	0.23	0.66	0.9	0.7
Producto  arrojado	45	104	297	405	315
Selección a realizar	1	2	4	6	4

 

Importante: La efectividadde este mecanismo depende de la capacidad de la función de adaptaciónpara discriminar los individuosmás aptos de los menos aptos. Engeneral se presentan problemas,

 

 

Renormalizaciónde la Función de Adaptación
 

Si al ejecutarun programa evolutivo aparece un individuo de muy alta adaptaciónen relación al resto de la población decimos entonces quese trata de un superindividuo. Ello puede ser causa de problemas:

• En primer lugar, este superindividuo será seleccionado para la reproducción con mucha más frecuencia que los demás, por tanto su material genético se propagará y el banco genético tenderá a hacerse homogéneo.
• En segundo lugar, nadie garantiza que esa mejor adaptación relativa del superindividuo en cuestión no sea mediocre en relación a la que se puede obtener mediante el proceso evolutivo.

En síntesis, un superindividuo puede conducir a la convergencia prematura de la dinámicaevolutiva por la pérdida de diversidad en el bancogenético debidaa la presión selectiva excesiva que ésteejerce.                                           

Por otra parte, aún sin que aparezcan superindividuos, cuando avanza la dinámica evolutiva las poblaciones tienden a homogeneizarse debido a la recombinación del material genético de los más aptos. Ello significa queenlos estadíos medios y avanzados del proceso los valores de la función de adaptación se "parecen", o dicho de otra forma, la función de adaptación tiende a perder su poder discriminante y con ello seperdería la emulación de la selección natural. En consecuencia, en esas etapas del proceso la selección se puede convertir en un proceso aleatorio con distribución prácticamente uniforme.                    

Parasolventarestos problemas se emplean técnicas como la renormalización de la función de adaptación.

Con la renormalización se busca lograr una diferenciación adecuada entre las adaptaciones de los individuos de la población, con el fin de atenuar los efectos de los superindividuos y de la uniformización. L. Davis (Handbook of Genetic Algorithms) propone tres técnicas para trabajar la adaptación:                   

• Identidad: Si la función de adaptación escogida no presenta los problemas potenciales antes descritos construya con ella la distribución de probabilidades para la selección.

• Ventana de renormalización: Es una modificación del valor de la adaptación que busca considerar iguales a aquellos individuos cuya aptitud esté por debajo de un valor mínimo que se requiere como parámetro. Se puede describir de la siguiente forma:
 
• Determine un mínimo(min) para la ventana de renormalización y asigne a cada cromosoma una adaptación nueva igual a max(min, adaptaciónvieja - min). La siguiente tabla ilustra un ejemplo con dos valores distintosdel parámetro min:
 
 

Adaptación vieja	500	200	110	80	20	5
Adaptación nueva si min=10	490	190	100	70	10	10
Adaptación nueva si min=100	400	100	100	100	100	100

 
 
• Renormalización lineal: Es una modificación del valor de la adaptación que otorga un nuevo valor de aptitud a cada individuo dependiendo de la jerarquia  relativa que ocupa en la población. Requiere de dos parámetros y se puede describir de la siguiente forma:

• Ordene los individuos por adaptación decreciente. Fije un valor máximo (TopRen) y un valor para el decremento (PasRen ). Al mejor individuoasígnele como nueva adaptación el valor TopRen. A losindividuos sucesivos en el orden establecido, asígnele una nueva adaptaciónque sea igual a la adaptación del precedente - PasRen. La siguiente tabla ilustra un ejemplo con dos juegos de parámetros distintos:
 
 

Adaptación vieja	500	200	110	80	20	5
Adaptación nueva si TopRen=100 y   PasRen=5	100	95	90	85	80	75
Adaptación nueva si TopRen=100 y PasRen=20	100	80	60	40	20	0

 

 

 
Operadores Genéticos                                                                     

Son los elementos de un programa evolutivo encargados de emular el proceso de reproducción de los individuos. Actúan sobre los cromosomas con el fin de recombinar o de alterar(levemente en lo posible) su información genética.                                              

Esencialmente existen dos clases de operadores genéticos:

• Unarios (tipo mutación): Crean un nuevo individuo mediante la introducción de un cambio pequeño sobre un cromosoma.Recalcamos que se procura que la alteración introducida sea leve.

• De orden superior (tipo cruce): Crean uno o más nuevos individuosrecombinando partes de varios (por lo menos dos) cromosomas. Emulanla reproducción sexual. En principio cada descendiente posee característicaspresentes en alguno de los padres.

Importante:  En general los operadores genéticos dependen fuertemente dela representación empleada.

   
 

Operadores de Mutación
 

A continuación revisaremos algunos ejemplos de operadores de mutación cuando la representación de un cromosoma es una cadena de símbolos que pertenecen a un alfabeto finito y luego revisaremos brevemente las propuestas de L. Davis (Handbook of Genetic Algorithms) para la representación de cromosomas mediante n-tuplas de números reales.
 

Mutaciones cuando la representación de un cromosoma es una cadena de símbolos que pertenecen a un alfabeto finito

Con una probabilidadde mutación definida a priori que constituye un parámetro del programa evolutivo (Pm), se procede a sortear cada posición (esto es cada gen) en el cromosoma para determinar si en ella habrá o no una mutación.

• Si el sorteo indica que no se produce una mutación el gen en cuestión permanece inalterado.

• En caso contrario, se procede a sustituir el contenido del gen por un elemento cualquiera del alfabeto en uso, el cual es escogido aleatoriamente con una distribución uniforme entre todos los elementos de ese alfabeto.

Un ejemplo en binario:

Se tiene definida laprobabilidad de mutacion de cada gen en el valor Pm=0.006 y sea un  cromosoma binario 10101010. La siguiente tabla indica los valores del sorteoefectuado para cada gen:

 

Cromosoma	1	0	1	0	1	0	1	0
Resultado del sorteo	0.1	0.005	0.034	0.34	0.056	0.43	0.67	0.02

 

Hemos destacado en negritas el único gen que va a mutar según el sorteo, pueses la única posición donde el valor sorteado (número aleatorio entre 0 y 1 encontrado con una distribución uniforme) es menoro igual que el parámetro Pm.

A continuación se sortea el elemento del alfabeto que va a ocupar ese gen. Supongamos que hacemos dicho sorteo al igual que antes en modo real (también puede hacerse en modo entero pues el alfabeto es finito). Para particionar el alfabeto de manera que todos sus elementos sean equiprobables, definimos que si elsorteo arroja un valor menor o igual que 0.5 entonces el elemento sustituto será el 0 y si es mayor que 0.5 el elemento sustituto será el 1. Al generar el número aleatorio correspondientese obtiene 0.76, por tanto el valor sustituto será el 1.

Setiene entonces queel cromosoma resultante de la mutación es 1 1101010 (en rojo el gen mutado).                      

 

Un ejemplo en octal:

Se tiene definida aprobabilidad de mutación de cada gen en el valor Pm=0.06 y sea un  cromosoma octal 10564330. La siguiente tabla indica los valores del sorteoefectuado para cada gen:

 

Cromosoma	1	0	5	6	4	3	3	0
Resultado del sorteo	0.1	0.005	0.034	0.34	0.056	0.43	0.67	0.02

 

Hemos destacado en negritas los genes que va a mutar según el sorteo, pues son las posiciones donde el valor sorteado (número aleatorio entre 0y 1encontrado con una distribución uniforme) es menor o igual que el parámetro Pm.

De nuevo seprocede a sortear el elemento del alfabeto que va a ocupar ese gen.Con finessimplemente ilustrativos, esta vez haremos dicho sorteo en modo entero. Paraparticionar el alfabeto de manera que todos sus elementos sean equiprobables, simplemente seleccionamos al azar con distribución uniforme un valor entre 0 y 7 y lo utilizamos como elemento sustituto. Al generar los números aleatorios correspondientes se obtiene 6, 0, 3 y 4 y en ese orden.                      

Se tiene entoncesqueel cromosoma resultante de la mutación es 1 6063 334 (en rojo los genes mutados).

 

Mutaciones  cuando el cromosoma es una n-tupla de números reales

Cuando el cromosoma viene dado por una n-tupla de números reales se pueden crear operadores en el espíritu de la mutación. L. Davis (Handbook of Genetic Algorithms) sugiere tres modalidades:

• Mutación aleatoria
• Mutación local corta o larga

La mutaciónaleatoria es semejante al caso anterior. Con una probabilidad de mutacióndefinida a priori que constituye un parámetro del programa evolutivo(Pm), se procede a sortear cada posición en el cromosoma para determinarsi en ella habrá o no una mutación.

• Si el sorteo indica que no se produce una mutación el gen en cuestión permanece inalterado.
• En caso contrario, se procede a sustituir el contenido del gen por un valor cualquiera escogido aleatoriamente con una distribución uniforme enel rango de búsqueda que corresponde a ese gen.

Un ejemplo:

Dada laprobabilidad de mutación en el valor Pm=0.006 y el cromosoma dadopor la cuatrúpla (1.07, 2.1, 4.08, 0.7). Los rangos de búsqueda paracada gen intervalos son los intervalos:
 

Cromosoma	1.07	2.1	4.08	0.7
Valor mínimodel rango	0	1.3	4	0
Valor máximodel rango	2	5	8	1

 

La siguiente tablaindica los valores del sorteo efectuado para cada gen:                     
 

Cromosoma	1.07	2.1	4.08	0.7
Resultado del sorteo	0.1	0.003	0.4	0.05

 

Hemos destacado en negritas el gen que va a mutar según el sorteo.

Ahora corresponde sortear el elemento del rango que va a ocupar ese gen. Para ello se sortea con probabilidad uniforme un valor en el intervalo [1.3, 5]. Supongamos que3.4 es el resultado del sorteo.

Se  tiene  entonces queel nuevo cromosoma resultante es (1.07, 3.4,4.08, 0.7) (en rojo el gen mutado).                     
 

 
En las mutaciones locales se define un parámetro que es el rango de mutación(el mismo para todos los genes) que no es otra cosa que el alcance máximode la perturbación. Dependiendo  del tamaño de este parámetrose habla de mutación local corta o larga.                      

Con una probabilidad de mutación Pm por gen previamente definida, se procedea sortear cada elemento de la n-tupla en el cromosoma para determinar si enél habrá o no una mutación.

• Si el sorteo indica que no se produce una mutación el gen en cuestión permanece inalterado.
• En caso contrario, se procede a sustituir el contenido del gen por un nuevo valor que se calcula sumándole o restándole una porción aleatoria del rango de mutación predefinido. El factor f que definelaporción aleatoria se escoge con una distribución uniforme entre-1 y 1,  de manera que defina también si se suma o se resta.

Un ejemplo:

Se tiene definida laprobabilidad de mutación en el valor Pm=0.06 y se tiene el cromosoma dadopor la cuatrúpla (1.07, 2.1, 4.08, 0.7). Se fijó 0.5 como rangode mutación para todos los genes.

La siguiente tablaindica los valores del sorteo efectuado para cada gen:                     
 

Cromosoma	1.07	2.1	4.08	0.7
Resultado del sorteo	0.1	0.03	0.4	0.65

 

Hemos destacado en negritas el gen que va a mutar según el sorteo.

Ahora corresponde sortear el factor que define la porción del rango a sumar, supongamos f=-0.34, entonces la perturbación que sufrirá el segundo gen es:

f x rangode mutación = -0.34x0.5 = -0.17

Asi el cromosoma resultante es (1.07, 0.4 ,4.08, 0.7) (en rojo el gen mutado).                     
 
 

 

Operadores de Cruce
 

Ahora presentaremos algunos operadores de cruce, al igual que antes diferenciaremos según el tipo de representación.
 

Cruces cuando larepresentación de un cromosoma es una cadena de símbolos quepertenecen a un alfabeto finito

Hemos planteado que el espíritu de los operadores de cruce es tratar de recombinarel material genérico de dos o más padres para producir nuevosdescendientes. En este espíritu se han propuesto diversos operadores cuando larepresentación de un cromosoma es una cadena de símbolos quepertenecen a un alfabeto finito, los más destados son:

• Cruce de unpunto
• Cruce de dospuntos
• Cruce uniforme

 
Cruce de un punto:

Opera mezclando el material genético de una pareja de cromosomas. Para producir losdos descendientes se procede así:

• Conprobabilidad uniforme se sortea un punto de cruce (Ptocru ) de forma tal que separe los cromosomas en dos secciones no vacias. A la secciónde la izquierda de cada padre la llamamos cabeza y a la derecha la llamamos cola del padre respectivo.
• El primer descendiente se forma con la cabeza del primer padre y la cola delsegundo, mientras que el segundo hijo se forma con la cabeza del segundo padrey la cola del primero.

Un ejemplo:

Sean los padres
 

 

P1:	x1	x2	x3	x4	x5	x6	x7	x8
P2:	y1	y2	y3	y4	y5	y6	y7	y8

 

Se sortea el puntode cruce el cual debe ser seleccionado entre 1 y 7 con probabilidad uniforme,sea por ejemplo Ptocru=5 y se intercambian las cabezas y las colas para producirlos hijos como se indica:

 

H1:	x1	x2	x3	x4	x5	y6	y7	y8
H2:	y1	y2	y3	y4	y5	x6	x7	x8

 
 
Cruce de dos puntos:

Opera también sobre una pareja de cromosomas. Para producir los dos descendientes se procede así:

• Con probabilidad uniforme se sortean dos puntos de cruce (Ptocru1   y PtoCru2) de forma tal que cada padre queda separado en tres seccionesno vacias. Al igual que en el cruce de un punto a la sección de la izquierda decada padre la llamamos cabeza y a la derecha la llamamos cola, la nueva zona del medio la llamamos centro del padre respectivo.
• Los descendientes se forman intercambiando los centros de ambos padres.

Un ejemplo:

Si se tienen los padres
 

 

P1:	x1	x2	x3	x4	x5	x6	x7	x8
P2:	y1	y2	y3	y4	y5	y6	y7	y8

 

Se sortean los puntos de cruceque deben ser seleccionados entre 1 y 7 con probabilidad uniforme, sea porejemplo Ptocru1=2 y Ptocru2 =5. Se procede a intercambiarloscentros para producir los hijos como se indica:

 

H1:	x1	x2	y3	y4	y5	x6	x7	x8
H2:	y1	y2	x3	x4	x5	y6	y7	y8

 
 
Cruce uniforme:

Opera recombinando el material genético de una pareja de cromosomas gen agen. A priori se define una probabilidad Pu, con la cual para producir losdos descendientes, se procede así:

• Con Pu se sortea cada gen, si el sorteo así lo indica se intercambian los genes homólogos de ambos padres, en caso contrario dichos genes permanecen inalterados.

Un ejemplo:

Si Pu=0,04 y setienen los padres
 

P1:	x1	x2	x3	x4	x5	x6	x7	x8
P2:	y1	y2	y3	y4	y5	y6	y7	y8

 

Se procede a hacer el sorteo gen a gen, supongamos que los resultados del sorteo son:
 

P1:	x1	x2	x3	x4	x5	x6	x7	x8
P2:	y1	y2	y3	y4	y5	y6	y7	y8
Resultados del sorteo	0.03	0.5	0.01	0.9	0.8	0.001	0.87	0.015

 

Hemosdestacado en negritas los resultados de los sorteos que obligan a intercambiar los genes, con lo cual se producen los hijos:                     

 

H1:	y1	x2	y3	x4	x5	y6	x7	y8
H2:	x1	y2	x3	y4	y5	x6	y7	x8

 
 

Cruces cuando elcromosoma es una n-tupla de números reales

L.Davis(Handbookof Genetic Algorithms) resume en dos los cruces para este tipo de representación:
 

• Cruce uniforme
• Cruce pesado

 
Cruce uniforme:

En elespíritu de los operadores de cruce, se busca recombinar el material genético de una pareja de cromosomas. A priori se define una probabilidad Pu, con la cual para producir los dos descendientes, se procede así:                      

• Con Pu se sortea cada gen y si el sorteo así lo indica, se intercambianlos genes homólogos de ambos padres, en caso contrario dichos genespermanecen inalterados.

Un ejemplo:

Si Pu=0,04 y setienen los padres:
 
 

P1:	1.07	2.1	4.08	0.7
P2:	2.01	1.8	3.82	0.9

 

Se procede a hacerel sorteo gen a gen con lo cual:
 

P1:	1.07	2.1	4.08	0.7
P2:	2.01	1.8	3.82	0.9
Resultados del sorteo	0.5	0.002	0.8	0.01

 

Se indicaron ennegrita los resultados que hacen intercambiar los genes. Finalmente se tienenlos siguientes hijos:
 

H1:	1.07	1.8	4.08	0.9
H2:	2.01	2.1	3.82	0.7

 
 

Cruce pesado:

A partir de dos padres se produce un único hijo que es el promedio de los padres. Para el cálculo del promedio se establece primero el peso que tendrá cada padre (un parámetro del método). Cada componente Hidel hijo se calcula con la siguiente relación:

p1 xXi + p2 x Yi

donde  Xi  y Yi son las componentes que ocupanla posición i en los padres X e Y y p1 y p2  son los pesos asignadosa X y a Y, respectivamente.

Un caso más general ocurre cuando se establece como parámetro una probabilidad Pppara sortear si el gen se va a promediar o no (en forma similar al cruce uniforme). Estopermitiría producir hasta dos hijos por cruce. Se procede de la siguiente forma:

• Con Pp se sortea cada gen y si el sorteo así lo indica, se coloca enla posición correspondiente el promedio obtenido , en caso contrario dichos genes permanecen inalterados.

Un ejemplo:

Si Pp=0,04 y setienen los padres:

P1:	1.07	2.1	4.08	0.7
P2:	2.01	1.8	3.82	0.9

 

Se procede a hacerel sorteo gen a gen y se tiene:
 

P1:	1.07	2.1	4.08	0.7
P2:	2.01	1.8	3.82	0.9
Resultados del sorteo	0.5	0.002	0.8	0.01

 

Se indicaron ennegrita los resultados que hacen promediar los genes. Finalmente se tienen lossiguientes hijos:
 

H1:	1.07	1.95	4.08	0.8
H2:	2.01	1.95	3.82	0.8

 
 
Debe resultar claro quesi Pp=1 se tiene el cruce pesado originalmente expuesto que sólo puedeproducir un hijo.                                                                          

 

 

Parámetros de Control
 

Para controlar ladinámica de un programa evolutivo se requiere de un conjunto de valoresque dependen del diseño mismo del programa, es decir de la combinación particular quese haya escogido en cuanto a representación, operadores, etc.                      

Típicamente son:

• Tamaño de población
• Probabilidad de cruce
• Probabilidad de mutación
• Tipo de renormalización con sus parámetros asociados
• Porcentaje de renovación de la población
• Probabilidad de selección de operadores

Hasta ahora hemos tratadoel uso de los primeros cuatro.                                                                    

Determinar el conjuntode parámetros adecuados para un programa evolutivo no es una tarea fácil,es en sí mismo un problema de búsqueda, pero en la  "entonación"adecuada reposa en mucho el rendimiento de un programa evolutivo.

 

Algoritmo Genético Simple
 

Por Algoritmo GenéticoSimple (AGS) nos referiremos a un programa evolutivo que tiene la estructuraoriginalmente sugerida por J. Holland et al:

Representación:	Binaria
Población:	De tamaño constante (n)
Inicialización:	Aleatoria
Renormalización:	Ninguna
Selección:	Rueda de ruleta
Operadores:	Cruce de un punto+ mutación
Sustitución:	Total
Parámetros:	n(~100), Pm(~0.002) y Pc (~0.8)

 

Esta es la estructura más elemental para un algoritmo genético.
 

Algunos detalles sobre la representación binaria

Nos referimos auna cadena de bits de longitud fija. Una cadena de bits puede construirse enLenguage C   a partirde las estructuras de datos estándar, por ejemplo

unsigned char	8 bits
unsigned int	16 bits
unsigned long	32 bits

El número debits a usar lo dicta la precisión deseada. Por ejemplo si la solución buscadaes un número real en el intervalo [0,1] y se desea una precisiónde6 cifras decimales, se debe dividir el intervalo en un millón de partes,por tanto la longitud del cromosoma sería:

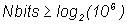
es decir, se debenusar 20 bits por lo menos

Para decodificarla representación a un número real en un intervalo [a, b] se utiliza la conocida correspondencia:

1. Convertir la cadena de bits de base 2 a base 10:


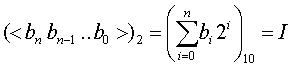
2. Calcular el valor real x correspondiente:

Esquema de reproducción del AGS                                                                          

La reproducción procede seleccionando pares de individuos por rueda de ruleta, se les cruza (haciendoel sorteo con  Pc) y luego se aplica la mutación (sorteo con Pm gen a gen) a ambos descendientes, es decir:
 
SELECCIÓN-CRUCE-MUTACIÓN (AMBOS HIJOS)

Importante:   La mutación aplica haya habidoo no cruce según el sorteo con Pc.

Esto se repite hasta completar unanueva población de n descendientes, para luego sustituir totalmente lapoblación anterior por la nueva.

 
Virtudes y defectos del AGS
 

El AGS presenta muchas virtudes, como por ejemplo:

• Es una metodología de  muy amplia aplicación y de fácil implantación.
• Es el programa evolutivo que ha sido estudiado en mayor profundidad.
• Es relativamente fácil de entonar a un problema particular.
• Los operadores genéticos son sencillos y de fácil comprensión.
• Requiere depocos parámetros.
• Con ligerasmodificaciones se puedeaumentar su rendimiento considerablemente.

pero también tienesus bemoles:                                                                          

• Su eficienciaes muy dependiente del diseño de la función de adaptación.

• El esquema desustitución total puede ocasionar la pérdida de la mejor soluciónalcanzada.
• Tiene tendenciaa la convergencia prematura por la presencia de algún superindividuo.
• La acciónconjunta de los operadores evolutivos no parece ser lo natural ni lo másconveniente.