
Computacion Emergente III:
Introduccion a los Automatas Celulares
Prof: Jose Ali Moreno

Computacion Emergente III:
Introduccion a los Automatas Celulares
Prof: Jose Ali Moreno
Clase1
INTRODUCCION Y DEFINICIONES BASICAS
- Definicion de un Automata
- Ejemplos de Automatas
- La Maquina de Turing
- Automata como Sistema Dinamico
- Aplicabilidad de los Automatas como sistemas Dinamicos
- Conceptos Basicos de Sistemas Dinamicos
- Ejemplos Simples de Simulaciones con Automatas
- Respuesta Normal del Sistema Inmune
- Modelo de Automata para la Respuesta del S.I. a la Presencia del virus de HIV
- Bibliografia
AUTOMATA ES UN DISPOSITIVO DE COMPUTO QUE OPERA COMO UNA MAQUINA DE ESTADOS FINITOS. ES DECIR DADA UNA ENTRADA PARTICULAR EL DISPOSITIVO ACCEDE A UNO DENTRO DE UN CONJUNTO FINITO DE ESTADOS (ALFABETO) DE ACUERDO A CIERTAS REGLAS DE TRANSICION.
TALES REGLAS DE TRANSICION QUE DETERMINAN EL ESTADO DEL AUTOMATA, A TODO TIEMPO t, EN GENERAL DEPENDEN DEL ESTADO ACTUAL Y DE LA ENTRADA EN ESE MOMENTO.
LAS REGLAS PUEDEN SER DE CARACTER ALEATORIO O DETERMINISTICO. EN CONSECUENCIA, SUELE HABLARSE DE AUTOMATAS DETERMINISTAS O ESTOCASTICOS.
LA DEFINICION DE UN AUTOMATA SE ESTABLECE A TRAVES DE LA ESPECIFICACION DE:UN AUTOMATA PUEDE PRODUCIR UNA SALIDA PERO EN GENERAL NO PUEDE ACCEDERLA, NI TAMPOCO POSEE MEMORIA PARA ACCESAR ALGUNA ENTRADA ANTERIOR.
- EL ALFABETO (ESTADOS ACCESIBLES)
- LAS REGLAS DE TRANSICION QUE DESCRIBEN LA RELACION ENTRE LAS ENTRADAS, EL ESTADO ACTUAL DEL DISPOSITIVO Y EL ESTADO QUE ESTE ACCEDE.
UN AUTOMATA DE ESTA CLASE PUEDE IMPLEMENTARSE POR UN DISPOSITIVO CON UNA CABEZA LECTORA, UNA CINTA CON LA SECUENCIA DE ENTRADAS Y UN PROGRAMA CON LAS REGLAS DE TRANSICION.
EN ESTE CASO EL DISPOSITIVO LEE EN CADA PASO DEL TIEMPO UN SIMBOLO DE ENTRADA, Y DE ACUERDO A LAS REGLAS DE TRANSICION, EN EL PROGRAMA, ACCEDE ALGUN ESTADO PERMITIDO.
EN NINGUN CASO PUEDE ACCESAR LA SALIDA QUE PRODUCE NI REGRESAR LA CINTA Y LEER UN SIMBOLO DE ENTRADA ANTERIOR.
Ejemplos de Automatas:
EXISTE UNA VARIEDAD DE EJEMPLOS PARA ESTA CLASE DE DISPOSITIVOS:
- COMPUERTAS LOGICAS: AND, OR, NAND, ETC.
- UNIDADES DE PROCESO DE UMBRAL COMO LAS DE M y P.
- EN GENERAL MUCHOS DE LOS MODELOS DE U.P.s EMPLEADAS EN REDES NEURONALES ARTIFICIALES.
- MAQUINAS EXPENDEDORAS AUTOMATICAS.
- MULTIPLEXERS.
- EN GENERAL CUALQUIER MAPEO DISCRETO.
- LA MAQUINA DE TURING
La Maquina de Turing:
A UN AUTOMATA SE LE PUEDE INCREMENTAR CONSIDERABLEMENTE SU PODER DE COMPUTO SI SE RELEJAN ALGUNAS DE LAS RESTRICCIONES IMPUESTAS.
POR EJEMPLO ES POSIBLE PERMITIR:
ESTAS EXTENSIONES PERMITEN CONFORMAR UN DISPOSITIVO MUY PODEROSO COMPUTACIONALMENTE: LA MAQUINA DE TURING, LA CUAL POSEE LA CAPACIDAD DE COMPUTO UNIVERSAL.
- LECTURA Y ESCRITURA SOBRE SU CINTA DE ENTRADAS
- REGRESA Y AVANZAR LA CINTA DE ENTRADAS
- EXTENDER INDEFINIDAMENTE LA DATA SOBRE LA CINTA DE ENTRADAS.
ES DECIR QUE ES UN DISPOSITIVO CAPAZ DE IMPLEMENTAR CUALQUIER PROCESO DE INFORMACIÓN ALGORITMICO.
EN LOS AÑOS 30 (ANTES DEL NACIMIENTO DE LOS COMPUTADORES DIGITALES) ALGUNOS MATEMATICOS EMPEZARON A PENSAR EL POSIBLE SIGNIFICADO DE QUE UNA FUNCION FUESE COMPUTABLE. Alonzo Church Y Alan Turing LLEGARON INDEPENDIENTEMENTE A CONCLUSIONES EQUIVALENTES.
LA MAS IMPORTANTE PUEDE PARAFRASEARSE ASI:"UNA FUNCION ES COMPUTABLE SI PUEDE SER CALCULADA POR UNA MAQUINA DE TURING"
UNA MAQUINA DE TURING ES MUY SIMPLE, PERO DESDE EL PUNTO DE VISTA LOGICO POSEE TODO LA POTENCIALIDAD DE CUALQUIER COMPUTADOR DIGITAL. PUEDE DESCRIBIRSE DE LA SIGUIENTE FORMA:
- PROCESA UNA CINTA INFINITA DIVIDIDA EN CUADROS, CADA CUADRO PUEDE CONTENER UN SIMBOLO DE UN ALFABETO FINITO CON LA RESTRICCION DE QUE EN LA CINTA SOLO PUEDE EXISTIR UN NUMERO FINITO DE TALES CUADROS CON SIMBOLOS.
- POSEE UN CABEZAL DE LECTURA/ESCRITURA QUE EN CUALQUIER INSTANTE DE TIEMPO ESTA POSICIONADO EN ALGUN CUADRADO DE LA CINTA.
- LA MAQUINA DE TURING POSEE TAMBIEN UN ESTADO INTERNO QUE ACCEDE VALORES SOBRE UN ALFABETO FINITO.
- FINALMENTE, EL ACCIONAR DE LA MAQUINA SE ESPECIFICA POR MEDIO DE UN CONJUNTO DE COMANDOS DE LA FORMA:
(estado_actual, simbolo_actual, nuevo_estado, nuevo_simbolo, izquierda/derecha)
LO QUE PUEDE INTERPRETARSE DE LA SIGUIENTE MANERA:
SI LA MAQUINA DE TURING ESTA EN EL estado_actual, Y EL SIMBOLO DEBAJO DEL CABEZAL LECTOR ES simbolo_actual, CAMBIAR SU ESTADO INTERNO A nuevo_estado, REEMPLAZAR EL SIMBOLO EN LA CINTA EN SU POSICION ACTUAL POR nuevo_simbolo, Y MOVER EL CABEZAL DE LECTURA ESCRITURA UN CUADRO EN LA DIRECCION INDICADA izquierda/derecha. SI UNA MAQUINA DE TURING ALCANZA UNA CONDICION PARA LA CUAL NO EXISTEN INSTRUCCIONES ESTA SE DETIENE.AL CONJUNTO DE INSTRUCCIONES DE UNA MAQUINA DE TURING SE LE DENOMINA PROGRAMA.
COMO PUEDE APRECIARSE DE LA DESCRIPCION ANTERIOR, UNA MAQUINA DE TURING ES MAS UN PROGRAMA (SOFTWARE) QUE UNA MAQUINA FISICA (HARDWARE). EN CONSECUENCIA UNA MAQUINA DE TURING PUEDE IMPLEMENTARSE EN UN NUMERO INFINITO DE DISPOSITIVOS FISICOS DE COMPUTO (ENTRE ELLOS AUTOMATAS CELULARES).
ES IMPORTANTE RECALCAR QUE LA PROPIEDAD DE COMPUTABILIDAD UNIVERSAL DE LAS MAQUINAS DE TURING ES VIABLE SOLO SI LA MAQUINA DE TURING DISPONE DE TIEMPO Y CINTA INFINITOS.
Automata como Sistema Dinamico:
ES POSIBLE ESTRUCTURAR UN SISTEMA DINAMICO DISCRETO CON UN AUTOMATA O UN CONJUNTO DE
ELLOS. TAL SISTEMA DINAMICO SERA DISCRETO EN DIVERSOS ASPECTOS:LA REGLA DINAMICA CORRESPONDIENTE SE EXPRESA COMO UNA RELACION FUNCIONAL RECURRENTE
- CONSISTE DE DISPOSITIVOS DISCRETOS.
- EVOLUCIONA EN PASOS DISCRETOS DE TIEMPO.
- EL CONJUNTO DE CONFIGURACIONES POSIBLES CONSTITUYE UN CONJUNTO FINITO.
ENTRE EL ESTADO DEL SISTEMA A TIEMPO t+1 Y EL ESTADO ANTERIOR A TIEMPO t.
LA REGLA DINAMICA DE CUALQUIER SISTEMA DINAMICO CONFORMADO POR AUTOMATAS PUEDE DESCRIBIRSE POR UNA ECUACION DE EVOLUCION DEL TIPO:
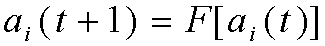
DONDE ai (t) REPRESENTA EL ESTADO DEL i-ESIMO AUTOMATA EN EL TIEMPO t Y F[ai (t)] ES UNA FUNCION DE LOS ESTADOS DE LOS AUTOMATAS QUE CONFORMAN EL SISTEMA EN EL TIEMPO t .
TAL TIPO DE SISTEMA DINAMICO OBSERVA UN COMPORTAMIENTO QUE PUEDE HACERSE TAN COMPLEJO COMO SE DESEE. (CONFIGURACION Y LEY DINAMICA)
Aplicabilidad de los Automatas como Sistemas Dinamicos:
A PESAR DE LA SIMPLICIDAD DE ESTOS SISTEMAS ES POSIBLE OBSERVAR EN ELLOS TODA LA RIQUEZA DE COMPORTAMIENTOS DINAMICOS QUE SE OBSERVA EN SISTEMAS COMPLEJOS:SON DE GRAN UTILIDAD EN LA SIMULACION DE SISTEMAS DINAMICOS REALES DE ALTA COMPLEJIDAD, DIFICILES DE SER ABORDADOS POR METODOS CONVENCIONALES.
- TRANSIENTES
- ATRACTORES : PUNTOS FIJOS
- CICLOS LIMITES
- CUASIPERIODICIDAD
- CAOTICOS
Conceptos Basicos de Sistemas Dinamicos:
LA DEFINICION GENERICA DE UN SISTEMA DINAMICO ES:
SEAUN CONJUNTO NO VACIO, Y SEA UNA CORRESPONDENCIA f: S----->S . DENOTAREMOS
POR f n LA COMPOSICION DE f n VECES CONSIGO MISMA, O SEA:
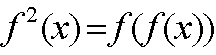
PARA UN x PERTENECIENTE A S (VALOR INICIAL)
EL CONJUNTO:
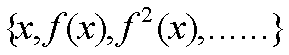
SE DENOMINA LA ORBITA DE x BAJO LA LEY DINAMICA f .
LA CORRESPONDENCIA TAMBIEN PUEDE ESCRIBIRSE PARA TIEMPO DISCRETO COMO UNA ECUACION
EN DIFERENCIAS:
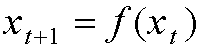
DONDE t = 0,1,2,.... Y x0 DENOTA AL VALOR INICIAL.
EN EL CASO DE UN SISTEMA DE AUTOMATAS S CORRESPONDE A UNA TUPLA DE VALORES TOMADOS
DE UN ALFABETO FINITO CON F[...] COMO REGLA DINAMICA.
EL CASO SEÑALADO SE REFIERE A SISTEMAS DINAMICOS DISCRETOS (BIEN t Y/O LOS ESTADOS x)
EL OBJETIVO DE CUALQUIER ESTUDIO DINAMICO CONSISTE EN LA IDENTIFICACION Y CARACTERIZACION DEL COMPORTAMIENTO ASINTOTICO (t MUY GRANDE) DE TALES SISTEMAS.
EJEMPLOS DE SISTEMAS DINAMICOS:
- ECUACIONES DIFERENCIALES ORDINARIAS CON EL TIEMPO COMO VARIABLE INDEPENDIENTE.
- MAPEOS TALES COMO EL LOGISTICO:
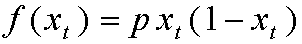
UN ATRACTOR DE LA DINAMICA PUEDE DEFINIRSE DE LA SIGUIENTE FORMA:
- SISTEMAS DE AUTOMATAS
- REDES NEURONALES, ETC.
UN PUNTO y ES UN PUNTO LIMITE DE x SI PARA CADA VECINDAD U DE y f(xt) REPETIDAMENTE ENTRA EN U CUANDO t -----> infinito.EL CONJUNTO L(x) DE TODOS LOS PUNTOS LIMITES DE x SE DENOMINA EL CONJUNTO LIMITE DE x, QUE EN GENERAL DEPENDE DE x.
UN CONJUNTO LIMITE L(x) ES ATRACTIVO SI EXISTE UNA VECINDAD ABIERTA U DE L TAL QUE L(x) = L PARA TODO x PERTENECIENTE A U. CONJUNTOS LIMITES ATRACTIVOS (ATRACTORES) SON LOS QUE SE OBSERVAN.
EN GENERAL OCURREN CUATRO CLASES DE CONJUNTOS LIMITES:
PUNTOS FIJOS O PUNTOS DE EQUILIBRIO QUE CORRESPONDEN AL CASO:
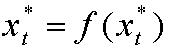
PARA TODO t.
CICLOS LIMITES CORRESPONDIENTES A LA SITUACION:
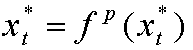
DONDE SE DICE QUE EL PUNTO x* ES PERIODICO DE PERIODO p.
LIMITE CUASIPERIODICO QUE CORRESPONDE A UNA DINAMICA EN LA CUAL LA ORBITA ES UNA SUPERPOSICION DE COMPORTAMIENTOS PERIODICOS CON FRECUENCIAS QUE SON SUMAS Y/O DIFERENCIAS DE UN CONJUNTO FINITO DE FRECUENCIAS BASE.
LIMITE CAOTICO, PARA EL CUAL NO EXISTE UNA DEFINICION ACEPTADA EXTENSAMENTE PERO QUE DESDE UN PUNTO DE VISTA PRACTICO PODRIA DEFINIRSE COMO “NINGUNA DE LAS ANTERIORES” ESTO ES UN COMPORTAMIENTO ASINTOTICO DE UNA ORBITA ACOTADA QUE NO ES UN PUNTO FIJO, O UN CICLO LIMITE U ORBITA CUASIPERIODICA.
Ejemplos simples de Simulaciones con Automatas:
UN AREA EN LA CUAL RECIENTEMENTE SE HA UTILIZADO MUCHO EL ENFOQUE DE SIMULACION CON AUTOMATAS ES EN EL ESTUDIO TEORICO DEL SISTEMA IMMUNE EN UNA APROXIMACION DE CAMPO MEDIO .Respuesta Normal del Sistema Inmune:
A PESAR DE QUE LOS TRABAJOS SON AUN MUY PRELIMINARES Y ELEMENTALES SI SE HAN PODIDO OBSERVAR, EN LOS MODELOS, COMPORTAMIENTOS ANALOGOS A LOS DEL SISTEMA REAL.
(M.Kaufman,J.Urbain y R.Thomas,J.Theoret.Biol. 114, 527 (1985) ; R.Thomas, J.Theoret.Biol. 153,1(1992)
EN ESTE EJEMPLO SE CONSIDERA UNA VERSION SIMPLIFICADA DEL SISTEMA INMUNE EN LA CUAL OCURREN CINCO COMPONENTES:TIPICAMENTE LA ACCION NORMAL DEL SISTEMA INMUNE ANTE LA PRESENCIA DE UN ANTIGENO ES, DE MANERA SIMPLIFICADA, LA DE DETECTAR Y ELIMINAR A LOS ANTIGENOS.
- LINFOCITOS B ........ B
- ANTICUERPOS. .....A
- LINFOCITOS AYUDADOR .....C
- LINFOCITOS SUPRESORES .....S
- VIRUS. .....V (ANTIGENO)
ESTE PROCESO INVOLUCRA LA ACTIVACION Y POSTERIOR DESACTIVACION DE LOS VARIOS ENTES COMPONENTES DEL SISTEMA.
PARA REPRESENTAR ESTE SISTEMA DE MANERA SIMPLE CON AUTOMATAS, CONSIDEREMOS AUTOMATAS BINARIOS (TOMAN VALORES DE UN ALFABETO BINARIO). SE DEDICA UN AUTOMATA PARA REPRESENTAR CADA COMPONENTE DEL SISTEMA Y LA SEMANTICA DE SUS ESTADOS ES QUE 1 REPRESENTA UNA ALTA CONCENTRACION DEL COMPONENTE RESPECTIVO MIENTRAS QUE 0 ES UNA MUY BAJA CONCENTRACION.
LAS REGLAS DE LA DINAMICA SE ESCRIBEN COMO EXPRESIONES BOOLEANAS DE LOS ESTADOS DE LOS DIVERSOS AUTOMATAS Y TRATAN DE REFLEJAR LAS OBSERVACIONES INMUNOLOGICAS.
LAS SIGUIENTES REGLAS PRESENTAN UN COMPORTAMIENTO DINAMICO RAZONABLE PARA LA REACCION NORMAL DEL SISTEMA:
t+1 t
A = B & C & V
B = (B | V) & C
C = C | not(S )& V
S = S | C
V = V & not(A
CADA ESTADO DE ESTE SISTEMA DINAMICO SE REPRESENTA POR UNA TUPLA DE CINCO COMPONENTES BINARIAS, POR ENDE EL NUMERO DE ESTADOS POSIBLES ES DE 32.
EN ESTE MODELO CADA ITERACION DE TIEMPO CORRESPONDE APROXIMADAMENTE A 103 HORAS DEL TIEMPO REAL.
LA SEMANTICA DE LAS REGLAS DE ESTE MODELO ES:
A = B & C & V
PARA SU PROLIFERACION, LOS ANTICUERPOS REQUIEREN LA PRESENCIA DE CELULAS B ASI COMO DE LINFOCITOS AYUDADORES Y VIRUSES.
B = (B | V) & C
LAS CELULAS B INCREMENTAN SU POBLACION CUANDO CUANDO ELLAS CONVIVEN CON VIRUSES Y EXISTEN LINFOCITOS AYUDADORES.
C = C | not(S )& V
LOS LINFOCITOS AYUDADORES SE FORMAN POR OTROS LINFOCITOS AYUDADORES O POR LA AUSENCIA DE LINFOCITOS SUPRESORES EN PRESENCIA DE ANTIGENOS.
S = S | C
LOS LINFOCITOS SUPRESORES SON FORMADOS POR ELLOS MISMOS O POR LA PRESENCIA DE LINFOCITOS AYUDADORES.
V = V & not(A)
LOS VIRUSES POR SU PARTE PROLIFERAN SI AUN EXISTEN Y NO HAY PRESENCIA DE ANTICUERPOS.
ESTA ULTIMA ES LA ECUACION CRUCIAL EN ESTE MODELO DE LA RESPUESTA NORMAL DEL S.I. ELLA IMPLICA LA LIQUIDACION DE LOS ANTIGENOS POR LOS ANTICUERPOS.
EN ESTE MODELO SE PUEDE VERIFICAR QUE LA DINAMICA CONDUCE A CINCO CONFIGURACIONES DE PUNTO FIJO PARTIENDO DE CUALESQUIERA DE LAS 32 CONFIGURACIONES INICIALES POSIBLES.
A PESAR DE LO SIMPLE DEL MODELO DINAMICO EL COMPORTAMIENTO NO DESVIRTUA AL REAL.A B C S V
(0 0 0 0 0) NINGUNA REACCION IMMUNE
(0 0 1 1 0) ESTADO VACUNADO O IMMUNE
(0 1 1 1 0) ESTADO VACUNADO O IMMUNE
(0 0 0 1 0) ORGANISMO DESPROTEGIDO
(0 0 0 1 1) ORGANISMO DESPROTEGIDO
Modelo de Automata para la Respuesta del S.I. a la Presencia del virus de HIV:
(R.B.Pandey,J.Stat.Phys,54,997(1989); J.Phys.I (France) 1;M.A.Nowak,J.Theoret.Biol,155,1(1992) )
EL OBJETIVO PARTICULAR EN ESTA CLASE DE MODELO ES EL DE SIMULAR COMO EL VIRUS HIV ES CAPAZ DE ELUDIR EL MECANISMO DE LA RESPUESTA INMUNE NORMAL. CONVIVIENDO EN EL SISTEMA ASI COMO LA NATURALEZA DE SU ESPORADICA PERO REPENTINA PROLIFERACION.
UN MODELO SIMPLIFICADO QUE PERSIGUE SIMULAR CON AUTOMATAS ESTE COMPORTAMIENTO INVOLUCRA INTERACCIONES ENTRE CUATRO COMPONENTES:
MACROFAGOS .....M: CELULAS CAPACES DE DESCOMPONER A LOS VIRUSES Y PRESENTAR EN SU SUPERFICIE COMPUESTOS CON PEPTIDOS DE LOS MISMOS (ANTIGENOS).
VIRUSES .....V: HIV
LINFOCITOS T AYUDADORES ....C
LINFOCITOS T CITOTOXICOS. ....X: QUE CONSTITUYEN LOS ELIMINADORES (TERMINATORS) DE ANTIGENOS EN EL SISTEMA.
LAS SIGUIENTES REGLAS CONDUCEN A UN COMPORTAMIENTO DINAMICO RAZONABLE PARA ESTA SITUACION:
EN ESTE EJEMPLO EL ESTADO DEL SISTEMA DINAMICO SE REPRESENTA POR UNA TUPLA DE CUATRO COMPONENTES BINARIAS, EL NUMERO DE ESTADOS POSIBLES ES DE 16.t+1 t
X = C & M & V
C = (C | M) & not(V)
M = M | V
V = (V | M | C) & not(X)
INICIANDO LA DINAMICA A PARTIR DE LOS 16 ESTADOS INICIALES POSIBLES SE ENCUENTRA QUE ESTA ALCANZA DOS PUNTOS FIJOS:
(0,0,0,0) Y (0,0,1,1)
ASI COMO UN CICLO LIMITE DE PERIODO TRES:
(0,1,1,1) -------(1,0,1,1)-------(0,0,1,0)-------(0,1,1,1)
LOS DOS PUNTOS FIJOS DESCRIBEN EL ESTATUS GLOBAL DEL SISTEMA INMUNE EN BASE A LAS INTERACCIONES APROXIMADAS QUE SE HAN SUPUESTO.
Bibliografia.
1-. E. Atlee Jackson,”Perspectives of Non-linear Dynamics”; vol. 2 Cap. 10,Cambridge University Press, Cambridge 1989
2.- T.Toffoli y N. Margolus,”Cellular Automata Machines”;The MIT Press, Cambridge Massachusetts 1987
3.- Alexander Schatten Cellular Automata Tutorial: http://www.ifs.tuwien.ac.at/~aschatt/info/ca/ca.html
4.-Pawel Siwak Cellular Automata:
http://staff.sk-kari.put.poznan.pl/siwak/Tutorials/CellularAutomata/index.html
5.- FAQ at the SantaFe Institute
http://alife.santafe.edu/alife/topics/cas/ca-faq/ca-faq.htm
6.- Collection of Papers from Stephen Wolfram
http://www.wolfram.com/s.wolfram/articles/indices/ca.html:
7.- Stephen Wolframs Homepage
http://www.wolfram.com/s.wolfram