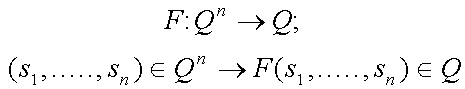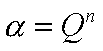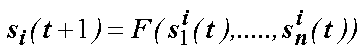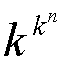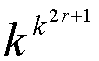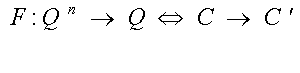LA DINAMICA DEL A.C. SE ESTABLECE POR
LA APLICACION SINCRONICA DE LA FUNCION DE TRANSICION LOCAL,
ESTO ES:
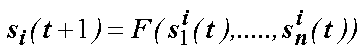
DONDE LOS ESTADOS
si
n PERTENECEN A NODOS DE LA VECINDAD DE
si.
ES CLARO DE LA DEFINICION ANTERIOR QUE LA DINAMICA DE LOS A.C.s
ES COMPLETAMENTE DISCRETA:
EL ESPACIO CELULAR ES UNA RED REGULAR QUE
PUEDE SER FINITA (CON CONDICIONES DE FRONTERA) O INFINITA.
CADA AUTOMATA, SOBRE LOS SITIOS DE LA RED, ACCEDE
SOLAMENTE ESTADOS DISCRETOS SOBRE UN ALFABETO FINITO CON EL TIEMPO
EVOLUCIONANDO A PASOS DISCRETOS.
EL ESTADO DEL A.C. (CONFIGURACION) SE DEFINE
EN CADA INSTANTE DE TIEMPO POR EL CONJUNTO DE VALORES DE ESTADO
{si} DE CADA
AUTOMATA EN LOS NODOS
{i}
DEL RETICULADO (
i = 0,1,........... SOBRE
TODO EL ESPACIO CELULAR, FINITO O INFINITO).
EL AUTOMATA EN CADA NODO
i-esimo
ASUME UN NUMERO GENERALMENTE PEQUEÑO (DIGAMOS
k ) DE VALORES.
si = 0,1,2,.......,k-1
(ESPACIO DE ESTADOS).
SI EL ESPACIO CELULAR (RED) ES BIDIMENSIONAL PUEDE
SER PREFERIBLE DENOTAR LOS ESTADOS POR:
sij
= 0,1,2,.......,k-1 USANDO DOS INDICES DE
POSICION (UN DETALLE POCO ESENCIAL).
AL DEFINIR UNA FUNCION DE TRANSICION
F SE DEBE ASOCIAR UN ELEMENTO UNICO
DE
Q CON CADA CONFIGURACION POSIBLE
DE LA VECINDAD. POR LO TANTO SE TIENEN
k = |Q| ESCOGENCIAS PARA CADA UNO DE LOS
kn ELEMENTOS
DE
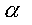
. LO QUE SIGNIFICA QUE EL NUMERO POSIBLE DE FUNCIONES
DE TRANSICION ES:
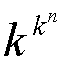
ESTE NUMERO PUEDE HACERSE CONSIDERABLEMENTE GRANDE
PARA VALORES MODERADOS DE
k Y
n . REFLEJANDO LA COMPLEJIDAD IMPLICITA EN ESTA
CLASE DE SISTEMAS.
EL VALOR DE ESTADO DEL
i-esimo
AUTOMATA EN EL INSTANTE DE TIEMPO SIGUIENTE DEPENDE DE LOS
ESTADOS ACTUALES DE LOS AUTOMATAS EN LOS NODOS PERTENECIENTES A
LA VECINDAD LA CUAL PUEDE INCLUIR AL VALOR DEL AUTOMATA
i-esimo .
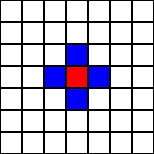
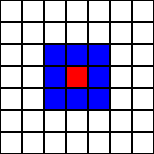
POR EJEMPLO, EN UN A.C. UNIDIMENSIONAL UNA VECINDAD
GENERICA PODRIA DENOTARSE POR EL CONJUNTO DE NODOS:
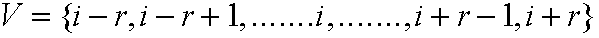
POR EJEMPLO PARA
r=5:

DONDE
r DENOTA EL RANGO
DE “INTERACCION” ENTRE LAS CELDAS.
EN ESTE EJEMPLO UNIDIMENSIONAL CON
k
ESTADOS POR CELDA SE TENDRAN
k2r+1
POSIBLES CONFIGURACIONES PARA LA VECINDAD. POR LO TANTO
EL NUMERO DE FUNCIONES DE TRANSICION POSIBLES SON:
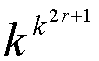
QUE EN ESTA CLASE DE A.C. CON
D = 1
, EL CASO MAS SIMPLE, CORRESPONDE A
k = 2
Y
r = 1 CON LO
CUAL EL NUMERO DE REGLAS DE TRANSICION POSIBLE ES DE
256. NO
ESTA DEMAS DECIR QUE ESTE ES EL TIPO DE A.C. MAS PROFUSAMENTE
ESTUDIADO, Y QUE NO OBSTANTE SU SIMPLICIDAD OBSERVA COMPORTAMIENTOS
DINAMICOS HARTO COMPLEJOS.
EN SU FORMULACION MAS ABSTRACTA LAS REGLAS DE TRANSICION
SE ESPECIFICAN EN TERMINOS DE UNA TABLA CON TODAS LAS POSIBILIDADES.
ESTO ES POR EJEMPLO EN EL CASO DEL A.C.
D = 1, r = 1
Y
k = 2:
000/C0
001/C1 010/C2
011/C3
100/C4 101/C
5 110/C6 111/C7
LOS
Ci DENOTAN
LOS VALORES DE LA CELDA CENTRAL EN EL SIGUIENTE PASO DE TIEMPO
Y LA REGLA DINAMICA SE ESTABLECE AL ESPECIFICAR CADA UNO DE ESTOS
VALORES.
UN
ASPECTO IMPORTANTE COMUN A LOS A.C.s ESTA
EN EL HECHO DE QUE LA
FUNCION DE TRANSICION TOMA VALORES DISCRETOS
SOBRE UN
CONJUNTO FINITO. ESTE HECHO, QUE RESTRINGE
LOS
VALORES POSIBLES DE LOS ESTADOS DE
LAS CELDAS A UN CONJUNTO PEQUEÑO ES LO QUE LOS DISTINGUE
DE OTROS SISTEMAS DINAMICOS TALES COMO LAS ECUACIONES DIFERENCIALES
PARCIALES.
ESTA CARACTERISTICA IMPLICA QUE LA
DINAMICA DE
LOS A.C.s ES SIEMPRE EXACTA, NO SE VE PLAGADA DE ERRORES DE
REDONDEO O DE APROXIMACION. ES DECIR DOS COMPUTADORES DIFERENTES
PRODUCIRAN SIEMPRE LA MISMA DINAMICA.
EL HECHO DE QUE LA DINAMICA ES EXACTA ES MUY IMPORTANTE
EN RAZON DE QUE POR EJEMPLO
OBSERVABLES QUE SE CONSERVAN
REALMENTE SE COMPORTARAN COMO TALES EN LAS SIMULACIONES (NO
PRESENTANDO VARIACION) .
A PESAR DE LA SIMPLIFICADA FUNCION DE TRANSICION LOS
A.C.s SON CAPACES DE OBSERVAR COMPORTAMIENTOS DINAMICOS SUMAMENTE
COMPLEJOS. TANTO ASI QUE SE HACEN ELUSIVOS AL ANALISIS MATEMATICO
DIRECTO EN LA ELUCIDACION DE SUS PROPIEDADES, QUEDANDO COMO UNICA
ALTERNATIVA EL RECURRIR A METODOS DE CARACTER EMPIRICO.
EN EL ESTUDIO DINAMICO DE LOS
A.C.s EL OBJETIVO ES POR SUPUESTO EL COMPORTAMIENTO DEL SISTEMA COMPLETO
EL CUAL SE DEFINE POR LOS VALORES DE LOS ESTADOS DE TODOS LOS AUTOMATAS
EN LAS CELDAS. A ESTE CONJUNTO DE ESTADOS INDIVIDUALES SE LE
DENOMINA
CONFIGURACION DEL SISTEMA:
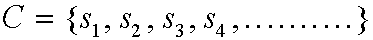
LA DINAMICA DEL A.C. PRODUCE CAMBIOS EN CADA
si ARROJANDO UNA NUEVA CONFIGURACION:
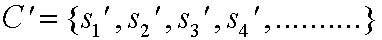
LA CORRESPONDENCIA
C----->C'
QUE SE PRODUCE, DENOMINADA TAMBIEN
CORRESPONDENCIA PARALELA
REPRESENTA LA
DINAMICA MACROSCOPICA
DE INTERES AL ESTUDIO DINAMICO. ES ESTA CORRESPONDENCIA LA QUE
DEFINE LA
ORBITA DEL A.C. EN EL ESPACIO DE CONFIGURACIONES
:
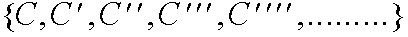
POR SU PARTE LA
FUNCION DE TRANSFERENCIA LOCAL
REPRESENTA LAS
REGLAS “MICROSCOPICAS”. EL MISTERIO
BASICO EN LA DINAMICA DE LOS A.C. ES, COMO VEREMOS, ESTABLECER LA
RELACION ENTRE:
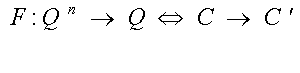
LOS ARGUMENTOS ANTERIORES SON INDICATIVOS DE QUE SALVO EN
ALGUNOS CASOS PARTICULARES EL NUMERO POSIBLE DE REGLAS DE TRANSICION
ES TAN ELEVADO QUE IMPIDE QUE CADA UNA DE ELLAS SEA INVESTIGADA
EXPLICITAMENTE. EN TAL SENTIDO LA METODOLOGIA QUE EN GRAN PARTE SE
EMPLEA ES LA DE LA “MUESTRA ESTOCASTICA” CON LA ESPERANZA DE QUE LAS
REGLAS DE TRANSICION ASI SELECCIONADAS CONDUZCAN A COMPORTAMIENTOS TIPICOS.
LOS FENOMENOS QUE SE IDENTIFIQUEN EN ESTE ENFOQUE EXPERIMENTAL PUEDEN
SER POSTERIORMENTE OBJETO DE APROXIMACIONES ANALITICAS U OTROS ANALISIS
MATEMATICOS CONVENCIONALES.
LA DETERMINACION DE PROPIEDADES GENERICAS ES IMPORTANTE
EN RAZON DE QUE SON INDEPENDIENTES DE LOS DETALLES PRECISOS DE
LA CONFORMACION DE LOS A.C. Y POR ENDE PUEDE ESPERARSE QUE SEAN UNIVERSALES
A UNA AMPLIA GAMA DE SISTEMAS INCLUYENDO AQUELLOS QUE OCURREN EN LA
NATURALEZA.
LOS METODOS DE LA TEORIA DE SISTEMAS DINAMICOS SON UTILES
EN EL ESTUDIO DE LAS PROPIEDADES GLOBALES DE LOS A.C.s PARA ELLO
SE CONSIDERA EL CONJUNTO DE CONFIGURACIONES (ORBITA) GENERADAS LUEGO
DE CIERTO TIEMPO A PARTIR DE CUALQUIER CONFIGURACION INICIAL.
LOS A.C.s SON MODELOS MATEMATICOS
UTILES EN SISTEMAS EN LOS CUALES MUCHOS COMPONENTES SIMPLES ACTUAN
CONJUTAMENTE PRODUCIENDO PATRONES COMPLICADOS DE COMPORTAMIENTO.
EN LA LITERATURA SE ENCUENTRA UNA AMPLIA VARIEDAD DE
APLICACIONES EN UNA GRAN GAMA DE DIFERENTES DISCIPLINAS: FISICA,
QUIMICA, BIOLOGIA, INFORMATICA, ECONOMIA, MEDICINA, SOCIOLOGIA, CIENCIAS
DE LA TIERRA, POR SUPUESTO EN MATEMATICAS, ETC. ALGUNAS DE ELLAS
SE IRAN PRESENTANDO A LO LARGO DEL CURSO.

Semantica de los Automatas Celulares:
EN GENERAL AL EMPLEAR UN A.C. COMO HERRAMIENTA DE MODELAJE
DE UN SISTEMA DINAMICO ES NECESARIO HACER UNA ABSTRACCION QUE ELIMINE
MUCHAS DE LAS COMPLICACIONES ORIGINALES PERO QUE A LA VEZ CONSERVE
LA MAYOR PORCION DE REALISMO POSIBLE EN EL MODELO.
COMO REGLA GENERAL ES QUIZAS UTIL ESTABLECER CIERTAS
ASOCIACIONES (SEMANTICA) ENTRE PARTES Y CARACTERISTICAS DEL SISTEMA
DINAMICO EN CUESTION Y SUS CONTRAPARTES EN EL MODELO DE A.C.s.
ALGUNAS DE LAS ASOCIACIONES COMUNMENTE EMPLEADAS SON:
EL ESTADO BASE DEL SISTEMA DINAMICO: EL ESTADO “VACIO”,
EL ESTADO FUNDAMENTAL, LA “SOPA PRIMORDIAL”, AUSENCIA DE ALGO, ETC.
LA CONFIGURACION BASE DEL A.C. CUANDO TODOS
LOS ESTADOS DE LOS AUTOMATAS si = 0
LAS LEYES DE LA DINAMICA: LEYES
FISICAS, QUIMICAS , BIOLOGICAS, ETC.
LA FUNCION DE TRANSICION.
LAS COMPONENTES ELEMENTALES (PRIMARIAS) DEL SISTEMA DINAMICO:
LOS TIPOS DE COMPONENTES ELEMENTALES QUE CONFORMAN EL SISTEMA:
ESTADOS DE LOS ATOMOS Y/O MOLECULAS, DE SPIN, ESTADOS DE SALUD O
DE ACTIVACION, TIPOS DE PRODUCTOS, ETC.
LAS CELDAS, O NODOS (AUTOMATAS)
DEL A.C. CON ESTADOS si
GENERALMENTE DISTINTOS DE 0. EL ESTADO
s i
DE CADA CELDA O AUTOMATA.
EL ESPACIO FISICO DONDE “VIVE” EL SISTEMA:
EL ESPACIO CELULAR.
EL ESTADO DEL SISTEMA TOTAL: CRISTAL, MOLECULA,
SISTEMA ECONOMICO, ETC.
LA CONFIGURACION DEL A.C. EN TODO EL
ESPACIO CELULAR, EL CONJUNTO DE ESTADOS s i
LA DINAMICA DEL SISTEMA:
LA CORRESPONDENCIA PARALELA
ES CLARO QUE ESTA ASOCIACION GENERAL CONSTITUYE EN LA MAYORIA DE
LOS CASOS UNA ABSTRACCION SEVERA DEL SISTEMA REAL.
POR EJEMPLO HAY RESTRICCIONES EN CUANTO A LA CAPACIDAD
DE REPRESENTACION DEL ARREGLO ESPACIAL, EN LA DISCRETITUD DE LAS
COMPONENTES Y DE LOS ESTADOS QUE ESTAS PUEDEN ACCESAR. NO OBSTANTE
ESTO, TAL SIMPLIFICACION EN GENERAL SE ASUME Y TRATA DE SER COMPENSADA
EN EL DISEÑO DE LAS REGLAS DINAMICAS.
ES DE NOTAR QUE SE HAN PROPUESTO SEMANTICAS MAS ABSTRACTAS
QUE LA ANTERIOR, QUE EN ALGUNOS CASOS SE DISCUTIRAN.

Bibliografia.
1-.
E. Atlee Jackson,”Perspectives of Non-linear Dynamics”;
vol. 2 Cap. 10,Cambridge University Press, Cambridge
1989
2.- T.Toffoli y N. Margolus,”Cellular Automata
Machines”;The MIT Press, Cambridge Massachusetts 1987
3.- Alexander Schatten Cellular Automata
Tutorial: http://www.ifs.tuwien.ac.at/~aschatt/info/ca/ca.html
4.-Pawel Siwak Cellular Automata:
http://staff.sk-kari.put.poznan.pl/siwak/Tutorials/CellularAutomata/index.html
5.- FAQ at the SantaFe Institute
http://alife.santafe.edu/alife/topics/cas/ca-faq/ca-faq.htm
6.- Collection of Papers from Stephen Wolfram
http://www.wolfram.com/s.wolfram/articles/indices/ca.html:
7.- Stephen Wolframs Homepage
http://www.wolfram.com/s.wolfram