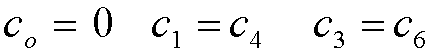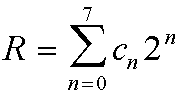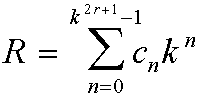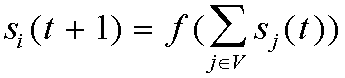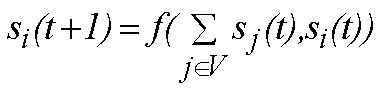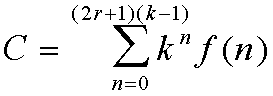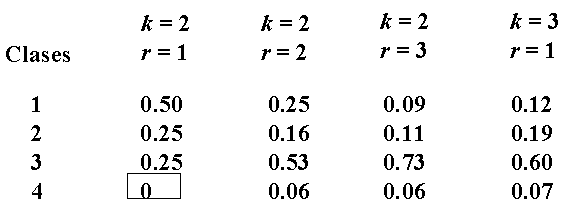Computacion Emergente III clase 3

Computacion Emergente III:
Introduccion a los Automatas Celulares

EN RAZON DE ESTA CONDICION EN LA FUNCION DE TRANSICION, F, UNA VEZ QUE EL A.C. ALCANZA LA CONFIGURACION EN LA CUAL TODOS LOS s_i = 0 , PERMANECE EN ESE ESTADO. (NINGUNA ACTIVIDAD SE PRODUCE A PARTIR DE ESTE ESTADO)

EN EL CASO DE A.C.s FINITOS (CON CONDICIONES DE BORDE) ESTA CONDICION ES REDUNDANTE MATEMATICAMENTE Y PUEDE OMITIRSE. ESTO ES CONSECUENCIA DE QUE TODOS LOS A.C.s FINITOS SON PERIODICOS. Toffoli (1977) MOSTRO QUE CUALQUIER A.C. FINITO ES EQUIVALENTE, BAJO UN CAMBIO DE ESCALA DE TIEMPO, A OTRO A.C. CON CONDICION BASE.

ii)EN GENERAL LA REGLA DE TRANSICION ES LOCAL PERO HOMOGENEA (NO DEPENDE DE LA POSICION i DE LA CELDA EN EL RETICULADO) SE DICE ENTONCES QUE EL SISTEMA POSEE UNA DINAMICA HOMOGENEA.

FRECUENTEMENTE SE SUPONE ADEMAS QUE LA DINAMICA TAMBIEN ES SIMETRICA. POR EJEMPLO EN 1D:

DONDE LA INVERSION SE REALIZA PARA TODO j. POR EJEMPLO:

EN EL CASO DE A.C.s DE MAYOR DIMENSIONALIDAD LA INVERSION ANTERIOR SE REEMPLAZA POR
INVARIANCIA DE LA REGLA DE TRANSICION BAJO ROTACIONES ALREDEDOR DE LA CELDA CENTRAL.

ESTAS RESTRICCIONES PARA LOS A.C. LEGALES REDUCEN EL NUMERO DE POSIBLES REGLAS DE TRANSICION. POR EJEMPLO EN 1D LA REDUCCION ES DE:

ESTE NUMERO REDUCIDO ES AUN TAN GRANDE QUE IMPIDE UN ESTUDIO SISTEMATICO DE TODAS ESTAS DINAMICAS POSIBLES.

ALGUNAS REGLAS DINAMICAS SE RELACIONAN ENTRE SI A TRAVES DE CIERTAS PERMUTACIONES SIMPLES ENTRE LOS k ESTADOS ACCESIBLES. EN ESTE CASO SE HABLA DE DINAMICA EQUIVALENTE POR PERMUTACIONES.

ES DE NOTAR QUE EN ALGUNAS SITUACIONES ES UTIL CONSIDERAR A.C.s SIN ESTADO BASE, INHOMOGENEOS O CON REGLAS DINAMICAS NO SIMETRICAS. ESTOS CASOS SE PRESENTAN CUANDO EN LA DINAMICA SE DESEAN INCLUIR INTERACCIONES CON AGENTES “EXTERNOS” TALES COMO FUERZAS EXTERNAS, REACTANTES QUIMICOS Y OTROS EFECTORES TALES COMO EL APRENDIZAJE.

ES DE UTILIDAD DEFINIR UN ESQUEMA DE NUMERACION QUE PERMITA IDENTIFICAR LAS DIFERENTES REGLAS DE TRANSICION POSIBLES DADO UN TIPO DE VECINDAD.

PARA ELLO CONSIDEREMOS PRIMERO EL CASO MAS SENCILLO CON k = 2 Y r = 1 EN UN A.C. 1D . EN
ESTE CASO HAY 3 CELDAS POR VECINDAD POR LO QUE LAS 8 POSIBLES CONFIGURACIONES SERAN:

111 110 101 100 011 010 001 000 t
c₇ c₆c₅ c₄ c₃ c₂ c₁ c₀ t +1

CADA c_i TOMA VALORES 0/1 (ESTADO A t+1 DE LA CELDA CENTRAL)

EN LA NOTACION ANTERIOR EL SUBINDICE DE LAS c SE HA ESCOGIDO IGUAL AL NUMERO REPRESENTADO POR LA CONFIGURACION DE LA VECINDAD EN BINARIO.

LAS POSIBLES TRANSICIONES s₁ s₂ s₃/c RECIBEN EL NOMBRE DE CONDICIONES DINAMICAS.

EL A.C. LEGAL SATISFACE LAS CONDICIONES DINAMICAS:

CON LO CUAL EL NUMERO DE CONDICIONES INDEPENDIENTES SE REDUCEN DE 8 A 5 Y CONSECUENTEMENTE EL NUMERO DE POSIBLES REGLAS DE TRANSICION.

LA NOTACION EMPLEADA EN EL CASO ANTERIOR SE PUEDE EXTENDER PARA CUALQUIER CONFIGURACION DE UNA VECINDAD EN UN A.C. 1D (CUALQUIER r Y k) ES DECIR ESTA SE PUEDE ASOCIAR A UN NUMERO CUANDO LA CONFIGURACION SE TOMA COMO DENOTANDO UN NUMERO k-ENARIO.

POR EJEMPLO SEA r = 2 Y k = 3:

Vecindad Notacion
02101 64
20001 163
11111 121

ESTA ES UNA FORMA CONVENIENTE PARA DENOTAR CUALQUIER CONFIGURACION DE UNA VECINDAD.

Notacion de Wofram:

DE LA MISMA MANERA ANTERIOR ES POSIBLE ASOCIAR UN NUMERO CON EL CONJUNTO DE VALORES DE ESTADOS CONSECUENTES (c₀,.........,c₇ ) EN LA REGLA DE TRANSICION. LA IDEA DE UN NUMERO DE REGLA DINAMICA LA INTRODUJO Wolfram (1984) (CASO BINARIO):

EL CUAL DEFINE LA CORRESPONDENCIA UNIVOCAMENTE.

CONSIDEREMOS ALGUNOS EJEMPLOS DE ESTO.

EL A.C. LEGAL DEFINIDO POR LA REGLA: 111/0 110/1 101/0 100/1 011/1 010/0 001/1 000/0 SE REPRESENTA POR EL NUMERO R = 2+8+16+64 = 90

MIENTRAS QUE EL A.C. “ILEGAL” 000/1 001/1 010/1 Y EL RESTO DE LOS c_n IGUALES A 0 CORRESPONDE A UN R = 1+2+4 = 7.

NOTAR QUE UNICAMENTE LOS A.C.s QUE NO CUMPLEN LA REGLA DE ESTABILIDAD POSEEN UN NUMERO DE REGLA DINAMICA IMPAR.

ES FACIL CONVENCERSE DE LA CONVENIENCIA DE DENOTAR LA DINAMICA DE ESTOS A.C.s POR MEDIO
DE ESTE NUMERO.

LA EXTENCION DE LA CONVENCION ANTERIOR A UN A.C. 1D GENERICO ES DIRECTA, ASI:

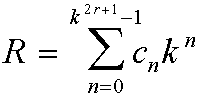
SI BIEN ESTE ESQUEMA DE NOTACION ES UNICO Y CONCISO ES PURAMENTE FORMAL, ES DECIR NO PROVEE INDICACION ALGUNA SOBRE LAS PROPIEDADES DE LA DINAMICA (CORRESPONDENCIA PARALELA) RESULTANTE DE LAS REGLAS CORRESPONDIENTES. EL ASOCIAR ALGUNA PROPIEDAD DINAMICA SUTIL CON R NO ES EN GENERAL TAREA FACIL.

EL NUMERO DE REGLA DINAMICA PUEDE SER GENERALIZADO PARA A.C. DE DIMENSIONALIDAD SUPERIOR BAJO LOS ESQUEMAS DE VENCIDAD TIPO I O TIPO II. EN ESTE CASO ES NECESARIO ESPECIFICAR UN ORDENAMIENTO LINEAL DE LOS ESTADOS EN LAS POSIBLES CONFIGURACIONES DE
LA VECINDAD Y APLICAR EL MISMO METODO ANTERIOR PARA DETERMINAR EL NUMERO R.

POR EJEMPLO EL “JUEGO DE LA VIDA” DE Conway ES UN A.C. 2D DE k = 2 CON VECINDAD TIPO II Y
REGLA DE TRANSICION TOTALISTICA EXTERIOR CORRESPONDIENTE A UN R = 224.

EL TERMINO SE REFIERE A AQUELLA CLASE DE REGLAS DE TRANSICION QUE SON FUNCION DE LA SUMA DE LOS ESTADOS DE LAS CELDAS EN LA VECINDAD:

POR SU PARTE LAS REGLAS TOTALISTICAS EXTERIORES SON AQUELLAS EN LAS CUALES EL ESTADO DEL SITIO CENTRAL DEPENDE SEPARADAMENTE EN LA SUMA DE LOS ESTADOS DE LAS CELDAS DE LA VECINDAD Y EN EL ESTADO DEL PROPIO SITIO:

Wolfram TAMBIEN SUGIRIO UN CODIGO PARA DENOTAR A LOS A.C.s 1D TOTALISTICOS:

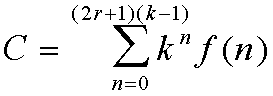
DONDE f(n) ES LA MISMA FUNCION QUE DEFINE AL A.C. TOTALISTICO, COMO f(0) = 0, ESTOS NUMEROS PUEDEN SER DIVIDIDOS POR k POR LO QUE SON INNECESARIAMENTE GRANDES. NO OBSTANTE, LOS VALORES DE C SON MUCHO MAS CONCISOS QUE LOS DE R (NO OCURREN MUCHOS VALORES DE C)

A CONTINUACION SE INDICA EL NUMERO DE REGLAS POSIBLES DE DIVERSOS TIPOS EN A.C.s 2D BINARIOS:

LOS ESTUDIOS REALIZADOS EN ESTE SENTIDO SOLO CONDUCEN A UNA CLASIFICACION CUALITATIVA DE LA DINAMICA DE LOS A.C.s.

PARA EL CASO DE A.C.s 1D, Wolfram (1983,1986) HA DETERMINADO LUEGO DE NUMEROSOS EXPERIMENTOS DE SIMULACION EN EL COMPUTADOR QUE PARA ESTADOS INICIALES “DESORDENADOS” (EL ESTADO DE CADA SITIO SE INICIALIZA ALEATORIAMENTE ENTRE 0 Y (k-1) CON PROBABILIDAD 1/k) SE MANIFIESTAN CUATRO COMPORTAMIENTOS CUALITATIVOS DIFERENTES:

D1: EVOLUCION A UNA CONFIGURACION ESPACIALMENTE HOMOGENEA (TODAS LAS CELDAS EN EL MISMO ESTADO).
D2: TENDENCIA EN EL TIEMPO A PATRONES CON ESTRUCTURAS FIJAS O PERIODICAS EN DIFERENTES REGIONES DEL ESPACIO.
D3: TENDENCIA A PATRONES CAOTICOS APERIODICOS EN TODO EL ESPACIO. PEQUEÑOS CAMBIOS EN LOS ESTADOS INICIALES CONDUCEN A DIFERENCIAS EN REGIONES CRECIENTES.
D4: EVOLUCION A PATRONES LOCALIZADOS COMPLEJOS, ALGUNOS DE LOS CUALES SE PROPAGAN DE MANERA IRREGULAR.

LOS A.C.s DENTRO DE CADA CLASE EVIDENCIAN UN COMPORTAMIENTO CUALITATIVO SIMILAR.

ESTE PEQUEÑO NUMERO DE CLASES SUGIERE UNA AMPLIA UNIVERSALIDAD EN EL COMPORTAMIENTO CUALITATIVO DE LOS A.C.s.

TAL UNIVERSALIDAD ES INDICATIVA DE QUE MUCHOS DE LOS DETALLES DE CONSTRUCCION SON IRRELEVANTES EN EL COMPORTAMIENTO CUALITATIVO (COMO LA CARDINALIDAD DEL CONJUNTO DE ESTADOS DE CADA SITIO ASI COMO EL TAMAÑO DE SU VECINDAD).

NO ES DESCABELLADO ENTONCES PROPONER LA CONJETURA DE QUE SISTEMAS DINAMICOS COMPLEJOS DE CARACTER BIOLOGICO O FISICO PUEDEN PERTENECER A LAS MISMAS CLASES DE UNIVERSALIDAD QUE ESTOS MODELOS MATEMATICOS ABSTRACTOS.

POR OTRA PARTE COMO LOS A.C.s PUEDEN CONSIDERARSE COMO SISTEMAS DE PROCESAMIENTO DE INFORMACION, EN LOS CUALES LA EVOLUCION DINAMICA IMPLICA LA EJECUCION DE UN COMPUTO SOBRE LA SECUENCIA DE VALORES INICIALES.

SE CONJETURA QUE LOS A.C. EN REGIMEN D4 SON CAPACES DE COMPUTABILIDAD UNIVERSAL.

Wolfram y Colaboradores (1984) TAMBIEN ESTUDIARON A.C.s TOTALISTICOS ENCONTRANDO QUE EXHIBEN LAS MISMAS CARACTERISTICAS DINAMICAS DE LOS OTROS A.C.s POR LO QUE NOCONSTITUYEN SIMPLIFICACIONES DINAMICAS.

ESTA OBSERVACION CORROBORA LA CONJETURA DE QUE LA CLASIFICACION ANTERIOR DEBE SER REPRESENTATIVA DE TODOS LOS COMPORTAMIENTOS DINAMICOS POSIBLES PARA A.C.s UNIDIMENSIONALES CON ESTADOS INICIALES DESORDENADOS. NO OBSTANTE AUN NO EXISTE PRUEBA FORMAL DE LA EQUIVALENCIA DINAMICA ENTRE A.C.s TOTALISTICOS Y GENERALES.

LA FRACCION APROXIMADA DE A.C.s TOTALISTICOS 1D PERTENECIENTES A CADA UNA DE LAS CLASES ANTERIORES DEPENDE DE k Y r SIENDO (Wolfram):

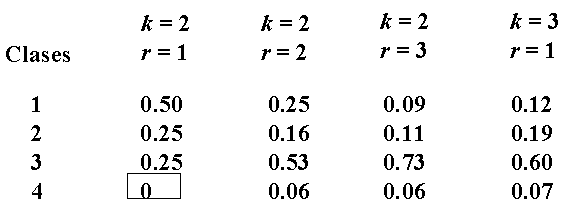
COMO SE NOTA NO SE ENCONTRO COMPORTAMIENTO TIPO D4 EN LOS A.C.s MAS SIMPLES.

EN PARTICULAR SE ENCONTRO QUE PARA k = 2 Y r = 2 LOS CODIGOS DE REGLAS OBSERVAN EL COMPORTAMIENTO DINAMICO SIGUIENTE:

D1: 0, 4, 16, 32, 36, 48, 54, 60, 62
D2: 8, 24, 40, 56, 58
D3: 2, 6, 10, 12, 14, 18, 22, 26, 28, 30, 34, 38, 42, 44, 46, 50
D4: 20, 52

RECORDAR QUE:

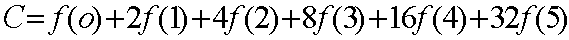
DONDE f(n) ES LA FUNCION DE TRANSICION QUE DEFINE LA DINAMICA.

LOS PATRONES CAOTICOS GENERADOS POR LAS REGLAS QUE OBSERVAN UN COMPORTAMIENTO TIPO D3 NO PRESENTAN EL MISMO “GRADO” DE CAOS. COMO EJEMPLO PUEDEN COMPARARSE LOS CORRESPONDIENTES A LAS REGLAS:

10: (0 1 0 1 0 0) 12: (0 0 1 1 0 0) 26: (0 1 0 1 1 0)

EL COMPORTAMIENTO DE LA REGLA 26 ES MAS O MENOS INTERMEDIO AL OBSERVADO CON LAS REGLAS 10 Y 12 . ESTAS DIFERENCIAS PUEDEN CUANTIFICARSE, COMO VEREMOS MAS ADELANTE, MIDIENDO DIVERSAS FORMAS DE ENTROPIA DE LOS PATRONES O LOS EXPONENTES DE LYAPUNOV DE LAS TRAYECTORIAS.

PARA EL CASO DEL COMPORTAMIENTO DINAMICO DE LA CLASE 4 EN GENERAL SE REQUIERE DE UN TIEMPO “GRANDE” PARA QUE SE ESTABLEZCA LA FORMA DEL PATRON (SIMPLE O COMPLEJA). ESTO INVOLUCRA UN PROCESO QUE ES UNA SUERTE DE BUSQUEDA EN EL ESPACIO DE CONFIGURACIONES HASTA QUE SE LOGRA ALCANZAR EL PATRON DE COMPORTAMIENTO CORRESPONDIENTE.

PARA UN EJEMPLO PUEDE CONSIDERARSE EL COMPORTAMIENTO DE LAS REGLAS 20:(0 0 1 0 1 0) O 52: (0 0 1 0 1 1). EN LOS CUALES PUEDE OBSERVARSE LA “EMERGENCIA” DE UNA AMPLIA GAMA DE PATRONES COMPLEJOS.

Clasificacion de las Propiedades Dinamicas de ACs con Estados Iniciales Deterministas (Numero Finito de Celdas Activas):

CUANDO SE CONSIDERAN CONFIGURACIONES INICIALES ESPECIFICAS (DETERMINISTAS) EN LUGAR DE LAS DESORDENADAS, ANTES DISCUTIDAS, RESULTA MUCHO MAS DIFICIL CARACTERIZAR EL COMPORTAMIENTO ASINTOTICO DE LOS PATRONES DINAMICOS Y MUCHO MAS CUALQUIERA DE SUS DETALLES. AUN RESTRINGIENDO LOS ESTADOS INICIALES DEL A.C. A UN NUMERO FINITO DE CELDAS ACTIVAS SE OBSERVA QUE DENTRO DE LOS COMPORTAMIENTOS YA DISCUTIDOS OCURREN DIVERSOS TIPOS O SUBCLASES CON DIFERENTES CARACTERISTICAS CUALITATIVAS:

F1: LOS PATRONES INICIALES DESAPARECEN EN EL TIEMPO (TIENDEN A UNA CONFIGURACION BASE).

F2: (a) LOS PATRONES INICIALES EVOLUCIONAN A UN ESTADO ESPACIAL DE TAMAÑO FINITO.
(b) LOS PATRONES INICIALES EVOLUCIONAN A UNA REGION EN EXPANSION UNIFORME QUE ES TOTALMENTE PERIODICA EN EL TIEMPO.
(c) LOS PATRONES INICIALES EVOLUCIONAN A UNA REGION EN EXPANSION UNIFORME QUE ES COMPLETAMENTE HOMOGENEA SALVO POR UNA REGION ESPACIAL FINITA.
F2: (d) LOS PATRONES INICIALES PRESENTAN FRONTERAS QUE SE EXPANDEN UNIFORMEMENTE PERO EL COMPORTAMIENTO DEL PATRON EN SU INTERIOR PUEDE SER CUALQUIERA DE LAS COMBINACIONES: CAOTICO, CAOTICO/PERIODICO O PERIODICO. EN EL CASO DEL PATRON CAOTICO/PERIODICO NO SE OBSERVA UN DESARROLLO UNIFORME EN EL TIEMPO.
F3: LOS PATRONES CAOTICOS CRECEN A TAMAÑOS INDEFINIDOS CON UNA TASA DE CRECIMIENTO ACOTADA POR r .
F4: LOS PATRONES CRECEN, SE CONTRAEN Y POSIBLEMENTE SE PROPAGAN DE MANERA IRREGULAR EN EL TIEMPO.

Bibliografia.

1-. E. Atlee Jackson,”Perspectives of Non-linear Dynamics”; vol. 2 Cap. 10,Cambridge University Press, Cambridge 1989

2.- T.Toffoli y N. Margolus,”Cellular Automata Machines”;The MIT Press, Cambridge Massachusetts 1987

3.- Alexander Schatten Cellular Automata Tutorial: http://www.ifs.tuwien.ac.at/~aschatt/info/ca/ca.html

4.-Pawel Siwak Cellular Automata:
http://staff.sk-kari.put.poznan.pl/siwak/Tutorials/CellularAutomata/index.html

5.- FAQ at the SantaFe Institute
http://alife.santafe.edu/alife/topics/cas/ca-faq/ca-faq.htm

6.- Collection of Papers from Stephen Wolfram
http://www.wolfram.com/s.wolfram/articles/indices/ca.html:

7.- Stephen Wolframs Homepage
http://www.wolfram.com/s.wolfram