Clase 10

MODELOS BÁSICOS DE COMPUTACIÓN NEURONAL: REDES A CAPAS (SEGUNDA PARTE)

· Aspectos y Limitaciones de las Redes a Capas

· Selección de la Arquitectura en las Redes Neuronales a Capas

Aspectos y Limitaciones de las Redes a Capas

Como ya hemos discutido, las redes a capas son capaces de aproximar arbitrariamente cualquier correspondencia no-lineal, a partir de un conjunto de ejemplos que la representen. Sin embargo, existe una serie de consideraciones prácticas que deben tomarse en cuenta:

a) ¿Cómo seleccionar la arquitectura y complejidad de la red?

b) ¿Qué representación de los datos se ha de emplear?

c) ¿Cuál es la capacidad de generalización de la red?

d) ¿Cómo es la complejidad de tiempo del aprendizaje?

En lo que sigue, se abordarán estos aspectos.

Selección de la Arquitectura en las Redes Neuronales a Capas

La selección del tamaño de la red es un aspecto importante en la práctica de las redes neuronales a capas: si la red es muy pequeña, no será capaz de sintetizar un buen modelo de los datos. Por el contrario, si ésta es muy grande, entonces será “demasiado capacitada”; es decir, podrá implementar numerosas soluciones, todas ellas consistentes con los datos de entrenamiento, pero la mayoría serán aproximaciones muy pobres del problema real (pobre capacidad de generalización).

En general, no se conoce qué complejidad ha de tener una red a capas para resolver algún problema dado. Aun más, es posible que este aspecto no pueda ser resuelto teóricamente en el caso general, ya que cada problema demanda diferentes capacidades de la red.

La recomendación, en el caso de poseer muy poca información a priori sobre el problema, es proceder por ensayo y error. Para ello, es útil emplear un enfoque metódico en el cual se comienza, bien con la red más pequeña posible, incrementando gradualmente su tamaño hasta que la calidad de ejecución de la red se nivele (es decir, no mejore sustancialmente), bien con una red muy grande que se “poda”, eliminando convenientemente UU. P.

Consideremos alternativas para el caso en que se comienza con la red más pequeña posible y se incrementa gradualmente su tamaño hasta que se nivele la calidad de ejecución. Este enfoque ha sido tratado por varios autores, para el caso de sintetizar una red que represente correctamente una función booleana (patrón de entrada binario de m componentes, junto con un patrón de salida binario de un solo componente). Se supone que el conjunto de entrenamiento no presenta ejemplos en conflicto (i.e., a cada patrón de entrada le corresponde un solo patrón de salida). Además, se supone que todas las UU. P. son unidades de umbral.

¿QUÉ ES UNA RED PEQUEÑA?

Existe un criterio heurístico para establecer la complejidad mínima de una red de una sola capa. Sean m el número de unidades de entrada (dimensión del patrón de entrada) y n el número de UU. P. de salida (dimensión del patrón de salida). Entonces, una red pequeña para este problema se conforma con un número de UU. P. en la capa escondida igual a:

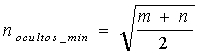
En la expresión anterior, la raíz cuadrada se redondea al número entero más cercano.

Tres esquemas para aumentar la complejidad de una R. N. A.

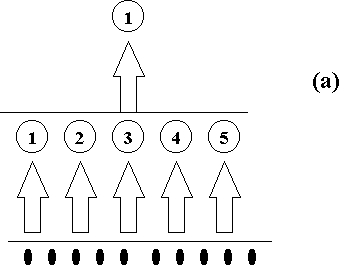
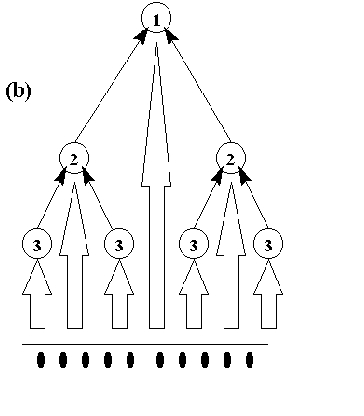
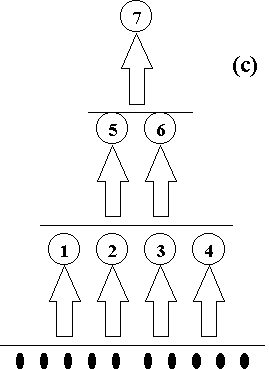
En el enfoque trivial, cada red de tamaño dado se entrena independientemente. Este proceso puede resultar muy costoso, pero si se ejecuta cuidadosamente, garantiza el encontrar la red más pequeña que resuelve la tarea.

Más eficiente sería utilizar un método dinámico. La idea en este caso consiste en agregar sucesivamente UU. P., a medida que son requeridas. Este enfoque difiere del anterior en que los nodos adicionales son incorporados durante el proceso de entrenamiento en la capa oculta (parte (a) de la figura arriba mostrada).

Para redes con una capa oculta, hay dos maneras sistemáticas a través de las cuales se puede lograr un "crecimiento dinámico de la red durante el entrenamiento”. La primera de ellas, versión simplificada, consiste en entrenar una red pequeña, y en caso de que no se resuelva el problema satisfactoriamente, se agrega una U. P. en la capa oculta y se reentrena la red, pero sólo se modifican los pesos sinápticos asociados con la nueva U. P. (i.e., los pesos alcanzados en el entrenamiento previo se congelan). Este procedimiento es bastante eficiente, pero, en general, no logra la solución óptima. La otra versión, denominada creación dinámica de nodos, involucra un reentrenamiento completo de cada nueva red, pero partiendo de los pesos anteriores como valores iniciales del nuevo proceso de aprendizaje. La decisión de agregar una nueva U. P. se toma considerando que, en general, el error cuadrático durante el entrenamiento por retropropagación disminuye con el tiempo. No obstante, cuando no se alcanza una solución, la tasa de decrecimiento disminuye de manera drástica; en ese momento debe agregarse una nueva U. P.

La condición para agregar un nuevo nodo se puede expresar así:

Donde: E(t) es el error cuadrático en el tiempo t, t_o es el tiempo en el cual se creó la neurona previa, d denota la porción de tiempo sobre la cual se calcula la pendiente de la curva E(t), y D_T es la pendiente de referencia (parámetro del método). El proceso se detiene cuando E(t) se hace lo suficientemente pequeña, o cuando se satisfaga algún criterio de terminación.

En los ensayos reportados, en muchos casos se alcanzó la arquitectura óptima previamente conocida. Un resultado importante es que el tiempo de aprendizaje fue, en el peor de los casos, un 40% mayor que el correspondiente al caso cuando se entrena de partida con la arquitectura óptima. En algunas situaciones fue hasta considerablemente menor.

Una pregunta abierta es si las soluciones de redes neuronales encontradas por este método también poseen propiedades óptimas de generalización con datos de entrada que “no han visto previamente”.

Otra propuesta consiste en un método sencillo que permite diseñar dinámicamente una arquitectura capaz de representar una correspondencia entre conjuntos de patrones, sin necesidad de aplicar el algoritmo de retropropagación del error. La idea es muy simple y consiste en agregar sucesivamente (i.e., en capas) sobre los nodos errados, UU. P. que son entrenadas cada vez con el algoritmo del Perceptrón o del ADALINE, hasta alcanzar la salida deseada. Este sería el método (c) de la figura arriba mostrada. En este proceso, el numero de UU. P. en capas sucesivas es menor cada vez, de tal forma que el proceso tiene fin. 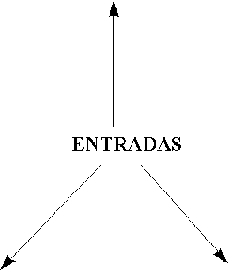Aquí se produce una división sucesiva, por hiperplanos, del espacio de patrones de entrada hasta lograr la separación total de los datos, como se ilustra en la siguiente figura:

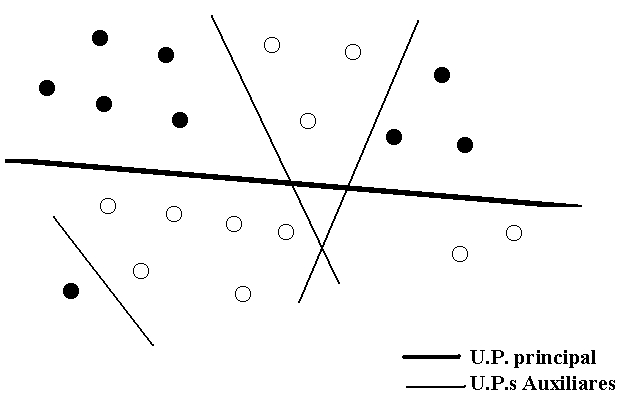
a) Se comienza con un Perceptrón simple de m entradas y una salida.

b) Se entrena la red con el algoritmo del Perceptrón. Esto conduce, en el peor caso, a que algunos ejemplos no sean aprendidos (puede optimizarse el número de ejemplos aprendidos).

c) Se divide el conjunto de entrenamiento en dos grupos que produzcan el mismo estado de la U. P. de salida (s1 = 1 y s1 = -1).

d) Se agrega una nueva neurona de salida (i.e., otro Perceptrón), y con los datos que producen la salida s1 = 1 se entrena para que produzca las correspondientes salidas deseadas "y".

e) Se repite el entrenamiento con el grupo de datos que antes presentaba salidas s1 = -1.

Si el resultado de estos dos pasos es que dos vectores de entrada con valores de salida deseados diferentes también correspondan a estados diferentes (s1 y s2) de las UU. P. de salida, entonces se ha logrado una representación “fiel” de la correspondencia booleana, aunque aún no sea la deseada. De lo contrario, hay que generalizar los pasos anteriores para aquellos grupos de ejemplos que producen la misma salida s1 y s2. La generalización consiste en dividir los datos de entrada en los grupos que producen el mismo estado de salida, y agregar una tercera neurona y entrenarla con cada grupo para que produzca la salida deseada, etc., hasta lograr una representación “fiel” de la correspondencia con las UU. P. (s1, s2, ..., sq) de salida, en el sentido antes explicado (i.e., que los patrones con diferentes salidas deseadas sean representados por diferentes estados de salida).

f) En este punto se inicia una nueva capa de salida con un Perceptrón de q entradas y una salida s1’. La nueva entrada la constituye ahora la capa previa de UU. P., y, utilizando el algoritmo del Perceptrón, se trata de aprender la relación:

De nuevo, si no hay éxito, hay que repetir para esta nueva correspondencia los pasos (a) - (f) descritos, agregando más UU. P. a la nueva capa de salida para perseguir una representación “fiel”.

La última capa debe estar formada por una U. P. que produzca correctamente la salida deseada para todas las entradas. Este proceso garantiza la convergencia, ya que puede mostrarse que en cada ciclo el número de UU. P. requeridas para producir una representación “fiel” de la correspondencia disminuye.

Este método es bastante eficiente ya que permite la utilización de UU. P. tipo McCulloch y Pitts de salidas bipolares.

La aparente complejidad de la arquitectura resultante se compensa con la simplicidad del algoritmo de entrenamiento. No deja de ser razonable imaginar que un mecanismo semejante ocurra en sistemas biológicos, donde un conjunto inicialmente pequeño de neuronas sea capaz de “reclutar” neuronas vecinas hasta alcanzar una red neuronal lo suficientemente grande para que sea capaz de aprenderse una tarea particular, a través de un mecanismo de aprendizaje simple de plasticidad sináptica tipo hebbiana.

Finalmente, la figura (b) muestra el tipo de arquitectura generada por el algoritmo de Frean (1990), el cual también fue diseñado para UU. P. binarias:

a) Se entrena una U. P. (U. P. # 1) con los datos, lo mejor que se pueda.

b) Se registran todos los casos que producen salidas incorrectas.

c) Se anexan dos nuevas UU. P. (UU. P. # 2), en caso de ser necesario: una, con la finalidad de corregir los casos +1 incorrectos; y la otra, los casos -1 incorrectos. Estas UU. P. secundarias tipo # 2 se conectan a la U. P. de salida tipo #1 a través de pesos grandes positivos o negativos. Esto con la finalidad de “vencer” la actividad previa incorrecta.

d) Las UU. P. tipo # 2 (conectadas a la entrada) se entrenan para ejecutar su tarea de corregir a la U. P. de salida, lo mejor posible.

e) Si es necesario, han de adicionarse UU. P. secundarias tipo # 3 para corregir los posibles errores de las UU. P. tipo # 2, y así sucesivamente. Cada U. P. adicionada reduce en al menos uno el número de patrones con salidas incorrectas. En este sentido, el proceso debe concluir en un tiempo finito. Puede demostrarse que la arquitectura jerárquica resultante de este proceso es equivalente a una R. N. A. de dos capas.

Otra posibilidad es comenzar con una red grande, y luego aplicar una técnica de poda a los pesos o nodos que poco contribuyen. En cualquier caso, es necesario reentrenar la red que ha sufrido el “daño neuronal”. Este proceso suele ser rápido, ya que se parte del estado previamente alcanzado.

Otra alternativa es utilizar un método dinámico de “poda” durante el proceso de aprendizaje. Esto se logra asignándole a cada conexión sináptica una tendencia a desaparecer, a menos que sea reforzada.

Al emplear estos enfoques, debe tenerse una idea de lo que significa una red grande para el problema en cuestión. Una cota superior del tamaño de red puede estimarse de acuerdo con lo siguiente:

a) En el Perceptrón Generalizado normalmente no se emplean mas de tres capas. En la mayoría de los casos basta con sólo dos. La red de R. B. F. siempre es de dos capas.

b) La cota superior para el número de nodos ocultos en el Perceptrón Generalizado de dos capas, para implementar los datos de entrenamiento exactamente, es del orden de p (número de ejemplos). Esto sugiere no utilizar más nodos ocultos que la cantidad de ejemplos de entrenamiento. En la práctica, el número de nodos ocultos debe ser mucho menor que p. De lo contrario, la red simplemente se “memoriza” los datos, dando como resultado una generalización muy deficiente.

Otra regla empírica de mucha utilidad en la estimación de la complejidad de la red tiene que ver con el número de parámetros (pesos y umbrales) necesarios. En general, es recomendable que este número no sea superior al número de ejemplos de entrenamiento.

El método más simple de implementar el algoritmo de poda dinámica consiste en utilizar las siguientes ecuaciones, luego de cada actualización de los pesos, para algún parámetro e pequeño:

Esto es equivalente a agregar un término de penalización del tipo a la función de error original E₀, y aplicar el método de descenso de gradiente sobre E:

Donde, el parámetro anterior e = gh.

El error anterior penaliza claramente la utilización de muchos pesos, pero también desanima tanto el empleo de pesos con valores grandes, que puede darse el caso de que un peso grande sea peor que muchos pequeños. Este inconveniente puede aliviarse con una función de error diferente:

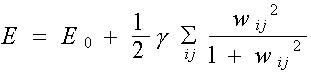
Lo cual es equivalente a que el parámetro e sea dependiente de los pesos:

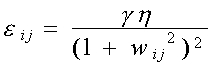
Con esta relación, los pesos pequeños decaen más rápidamente que los grandes. Estos métodos son eficientes en la eliminación de conexiones innecesarias, pero muchas veces lo que se desea es la eliminación de UU. P. completas. Para proceder con esto, se puede tratar de que los pesos de UU. P. con salidas pequeñas o con pesos poco significativos decaigan más rápidamente. Una forma es reemplazar la expresión de e por la siguiente, utilizando la misma e_i para todos los pesos de la i-ésima U. P.: