Clase 2
MODELOS BÁSICOS DE COMPUTACIÓN NEURONAL (PRIMERA PARTE)
· Primeros Modelos de Computación Neuronal
· Regla de Aprendizaje del Perceptrón
· Teorema de Convergencia para la Regla de Aprendizaje del Perceptrón
· Variantes de la Regla del Perceptrón
· Visualización Geométrica de la Regla del Perceptrón
· Perceptrón con UU. P. en Competencia
Primeros Modelos de Computación Neuronal
La creciente disponibilidad de poder de cómputo barato ha permitido la popularización del estudio de simulaciones de algunos modelos de computación neuronal; particularmente, en lo que respecta a la capacidad de ciertas reglas de aprendizaje, así como a la eficiencia del cómputo.
De estos modelos iniciales repasaremos:
·
PERCEPTRÓN
(Rosenblatt, 1958)
·
ADALINE (Widrow, 1962)
· MATRIZ DE MEMORIA ASOCIATIVA (Willshaw, 1969)
El Perceptrón
Es un dispositivo determinista que consta de un número arbitrario de capas. El Perceptrón Simple (P. S.) es el más elemental de todos: dispone de una sola capa y su modo de entrenamiento es del tipo supervisado.
Los dispositivos tipo P. S. consisten en un número fijo (n) de UU. P., cada una con m líneas de entrada por las cuales reciben patrones m‑dimensionales, cada uno de los cuales está correlacionado con un patrón n‑dimensional binario o bipolar.
El dispositivo debe ser capaz de aprender la correlación entrada‑salida. En términos matemáticos, los conjuntos de entrada y de salida definen una relación y el Perceptrón debe sintetizar una representación de la misma.
En general, los dispositivos neuronales a capas se denominan redes neuronales relacionales.
El cómputo que ejecuta el Perceptrón, para el caso de salidas binarias, es:
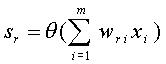
Donde: sr es la salida de la r‑ésima U. P., xi es la componente i‑ésima del patrón de entradas y wri es el peso sináptico correspondiente a la i‑ésima entrada de la r‑ésima U. P.
Si la salida es bipolar, el cómputo del Perceptrón es:
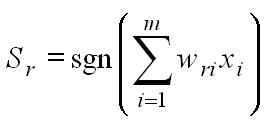
La función de transferencia en este caso es la función signo (sgn), la cual produce, a la salida, el signo de su argumento (en este caso, el potencial presináptico).
Es de notar que el conjunto de pesos sinápticos para una U. P. constituye una tupla m‑dimensional, al igual que los patrones de entrada. En tal sentido, al considerarse como vectores, pertenecen al mismo espacio m‑dimensional. Como consecuencia, el cómputo se expresa más fácilmente como:
![]()
El argumento de las
funciones de transferencia es el producto escalar entre el vector de
pesos (W) y el vector de entradas (X).
Condición de Funcionamiento del Perceptrón
Es fácil ver que para que el Perceptrón ejecute la tarea de relacionar el conjunto de entradas con las salidas, el vector de pesos w ha de escogerse de tal manera que la proyección de cada uno de los patrones de entrada x sobre w tenga el mismo signo que el de su correspondiente salida deseada z (o que sea negativo para salida 0 y positivo para salida 1, en el caso binario).
Para el caso bipolar,
en particular, el correcto funcionamiento del dispositivo requiere simplemente
que el signo del potencial presináptico sea el mismo que el de la salida
correspondiente.
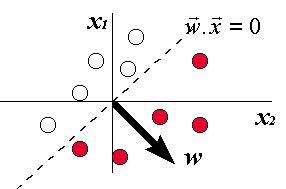
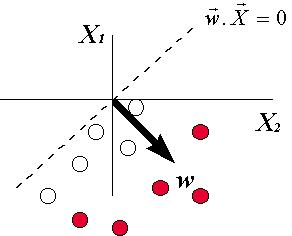
La frontera entre
proyecciones negativas y positivas de x sobre w es el
plano w×x = 0, que pasa
por el origen y es perpendicular al vector w. Por lo tanto, la condición de
correcta operación del Perceptrón es que este plano divida al conjunto de
entradas en dos subconjuntos, de manera que cada uno agrupe las entradas
asociadas a un mismo tipo de salida:
Una formulación alternativa para salidas bipolares, redefiniendo los vectores de entrada como:
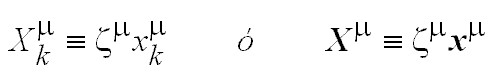
con lo cual se involucra en un solo patrón tanto la entrada como la salida, se obtiene para la condición de funcionamiento:

para todo m. Esto significa que todos los vectores X deben estar del mismo lado del
plano perpendicular al vector de pesos sinápticos w.
Separabilidad Lineal
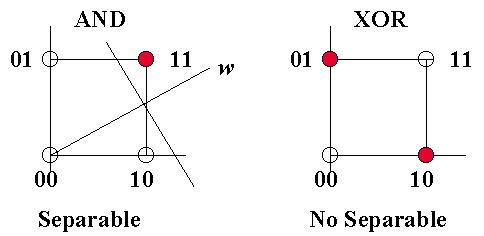
Si un plano separador como los indicados anteriormente no existe, entonces el Perceptrón es incapaz de realizar la tarea de cómputo, independientemente de cómo sea entrenado. En otras palabras, la condición para que el Perceptrón simple resuelva un problema es que éste sea linealmente separable.
Un problema es linealmente separable, si en el espacio de patrones de entrada se puede encontrar un hiperplano (de dimensión m - 1) que separe los patrones de una clase (+1) de los de la otra clase (-1 ó 0).
Si el dispositivo consta de más de una U. P., entonces esta condición de separabilidad lineal debe cumplirse para cada una de ellas.
Ejemplos de separabilidad lineal:
Inclusión del umbral. Hasta ahora, en las expresiones, hemos considerado UU. P. en las cuales o bien el umbral es cero o bien se coloca implícitamente como una componente adicional en el vector de pesos sinápticos (típicamente, la componente cero) junto con la señal de entrada correspondiente fija en el valor -1 en el patrón de entrada:
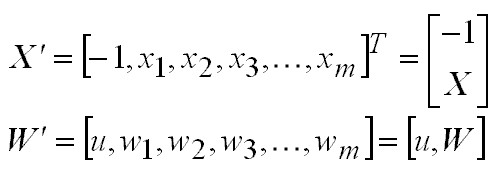
Para estos casos, el plano separador debe pasar por el origen de coordenadas. Si, por el contrario, el umbral se considera explícitamente en el cómputo de la U. P., entonces:
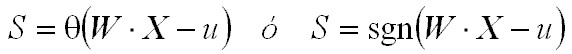
Y, consecuentemente, las regiones del espacio de patrones correspondientes a distintas clases deben estar separadas por el hiperplano:
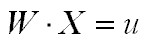
Lo que significa que
el plano separador es perpendicular al vector de pesos W, pero está a una distancia u del origen.
Regla de Aprendizaje del Perceptrón
La tarea consiste en determinar los pesos sinápticos para que el dispositivo represente la relación entrada‑salida lo más fidedignamente posible.
En caso de existir una solución, existe una regla iterativa de aprendizaje que permite corregir los pesos sinápticos para que éstos alcancen los valores deseados, partiendo de un conjunto de pesos inicializados aleatoriamente. Ésta es (para el caso de salidas binarias):
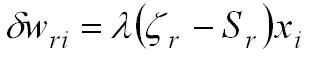
Mientras que, para el caso de
salidas bipolares:
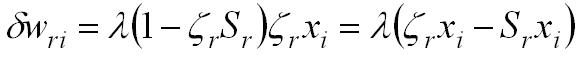
donde: l es el parámetro de aprendizaje (l << 1). zr es la componente r‑ésima del patrón de salida deseado.
La regla del Perceptrón puede interpretarse como "la combinación correcta de estímulo‑reacción se aprende; toda combinación incorrecta se olvida".
Para un conjunto de k patrones de entrada, la corrección de los pesos puede realizarse según las siguientes ecuaciones:
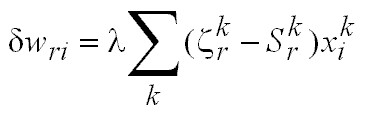
Esto corresponde al entrenamiento
por lotes.
Teorema de Convergencia para la Regla de Aprendizaje del Perceptrón
Supongamos que la
relación de entrada-salida puede representarse con un conjunto adecuado de
pesos w*ri y que los patrones de entrada x están acotados:
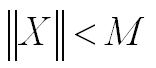
Entonces, la regla de aprendizaje del Perceptrón, con un parámetro de aprendizaje:
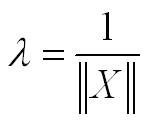
converge hacia la solución, luego de un número finito de pasos de corrección de los pesos.
Demostración: consideremos una sola U. P. (son independientes). Denotemos el vector de pesos que representa la relación entrada-salida por:
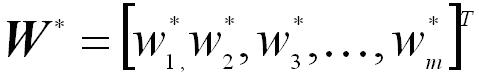
lo cual significa que existe una
constante positiva a, tal que:

Denotemos
respectivamente por

el vector de pesos del Perceptrón después de t correcciones y la diferencia entre la salida deseada y la salida real del dispositivo, en caso de error.
Para un paso de corrección se tendrá lo siguiente:
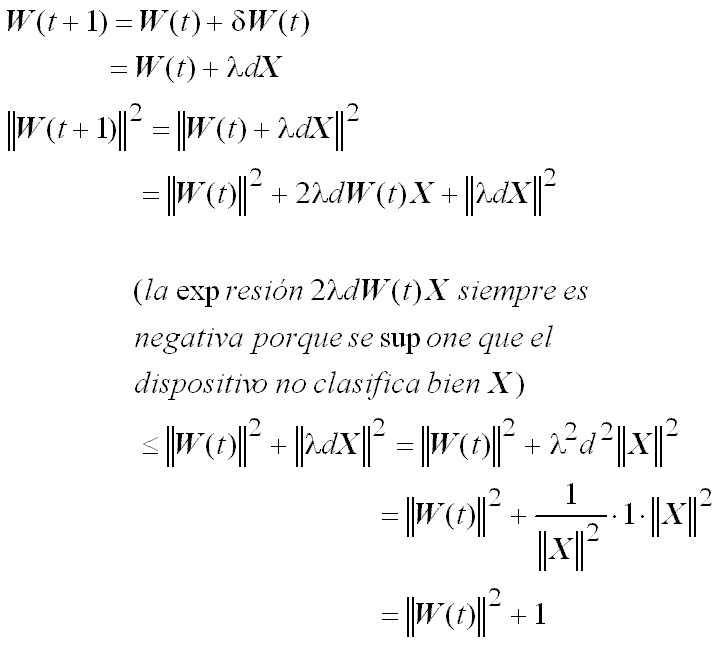
Esta última desigualdad establece una cota superior para el crecimiento del módulo del vector de pesos con las sucesivas correcciones de aprendizaje:
.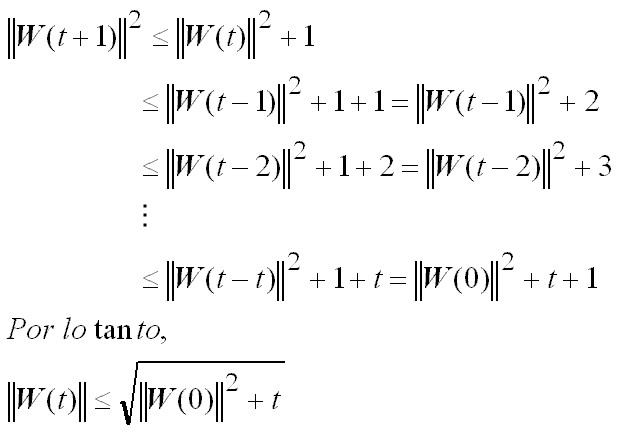
Por otra parte, para cada paso de corrección, también se cumple lo siguiente:
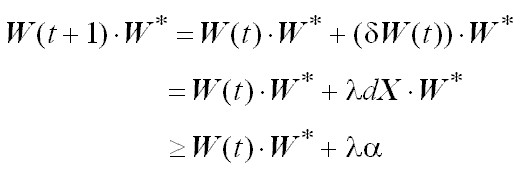
Es decir el producto w(t) × w* al menos crece de manera lineal con
t (número de pasos de corrección):
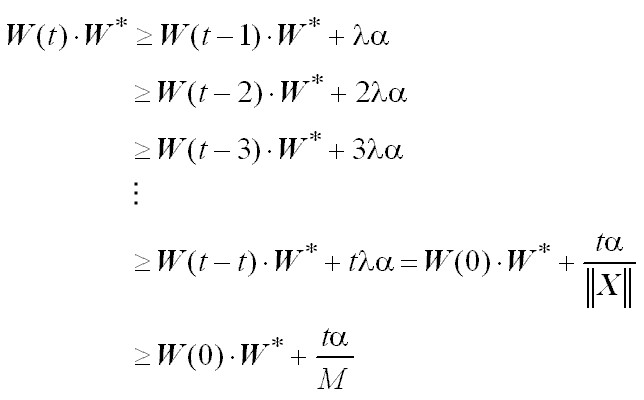
Haciendo uso de las
dos desigualdades establecidas y de la desigualdad de Cauchy‑Schwarz
tenemos:
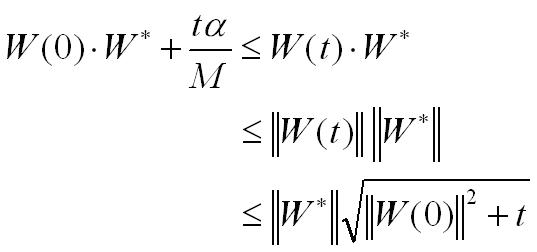
El lado izquierdo de la expresión anterior es lineal en t, y, por ende, de crecimiento mayor que el lado derecho. Esto implica que t no puede crecer arbitrariamente; o sea, el número de pasos de corrección t debe ser finito.
El Perceptrón, por su simplicidad
e independencia de UU. P., permite una serie de análisis teóricos que arrojan
mucha luz en cuanto a su eficacia y limitaciones como máquina de aprendizaje
(Minsky y Papert, 1969). Esto no es característico de otros dispositivos
neuronales. No obstante, los resultados teóricos obtenidos sobre el Perceptrón
son de importancia porque ilustran en gran medida la problemática a la que nos
enfrentamos con la metodología.
Variantes de la Regla del Perceptrón
En lugar de exigir que
el signo del potencial presináptico (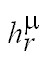 ) de la unidad de salida sea
el correcto
) de la unidad de salida sea
el correcto
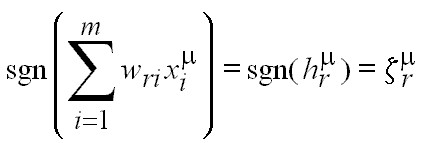
una buena alternativa es exigir que
su “tamaño” sea mayor que algún valor:
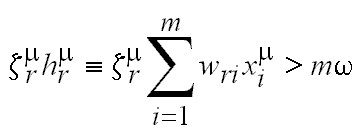
El margen positivo
fijo w es útil porque
proporciona una zona muerta que hace más robusta la frontera de decisión. Es
decir, el hiperplano de decisión del Perceptrón es forzado a estar situado en
una región entre las dos clases tal que exista suficiente espacio entre el
hiperplano y los puntos extremos del conjunto de entrenamiento. Esto fortalece
al Perceptrón frente a entradas ruidosas.
Como la sumatoria sobre i escala con la dimensión de los patrones de entrada (m), se
incluye este valor a la derecha de la expresión para mantener fijo el valor del
parámetro w.
Esta idea puede implementarse incluyendo la restricción de escala en la
siguiente regla de aprendizaje:
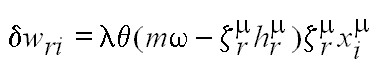
la cual se aplica cada vez que falle la condición de
escalamiento (esta acción la provoca la función de escalón de Heaviside q(×) que
involucra en su argumento la condición de escalamiento). La regla estándar del
Perceptrón (salvo por un factor de dos en l) se obtiene de la anterior cuando w = 0.
Visualización Geométrica de la Regla del Perceptrón
Consideremos una sola U. P., así como los patrones de entrada redefinidos X, por lo que:
![]()
Esta regla establece
que el vector de pesos w se
actualiza en una fracción del vector X, si su proyección w×X es menor que m k / |w|. El proceso se itera muchas veces hasta que todas las
proyecciones sean lo suficientemente grandes, estableciéndose así la dinámica:
w
® w’
® w’’
® w’’’
que se puede esquematizar para k = 0:
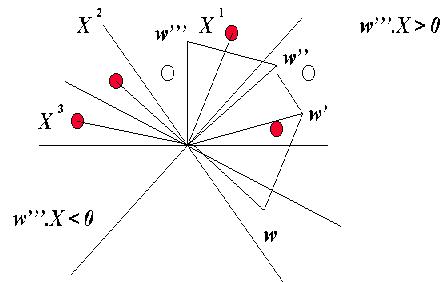
Es de esperar que al final
de esta dinámica de entrenamiento no haya patrones en la región
"mala" del espacio (w'''×X < 0). Para cualquier valor de k, una dirección de w para la cual sus proyecciones sobre
los vectores patrón X son
positivas es una solución potencial, salvo un factor de escala en |w| (no hay dependencia del módulo del vector de pesos).
Dificultad de un Problema
Dependiendo de los
patrones X, podría haber muchas de tales
direcciones de w
solución (cono amplio de direcciones) o pocas de ellas (cono angosto de
vectores de peso solución) o hasta ninguna (no hay solución posible). Las
figuras siguientes muestran dos ejemplos de los primeros dos casos:
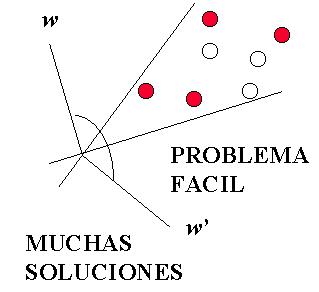
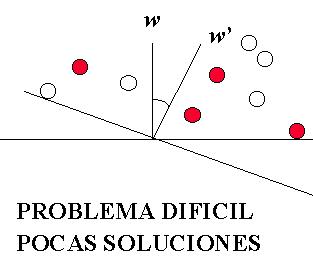
El hecho de que pueden existir muchas direcciones (o ninguna) de w para resolver un problema, permite la definición de un criterio para cuantificar el grado de dificultad del problema:
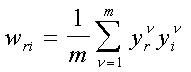
El criterio se define
en términos de la peor de las proyecciones; o sea, de la distancia del peor patrón
X al plano perpendicular al vector de
pesos w. Si D(w) > 0, entonces todos los patrones están en una zona buena, por
lo que puede encontrarse una solución para algún |w|
grande.
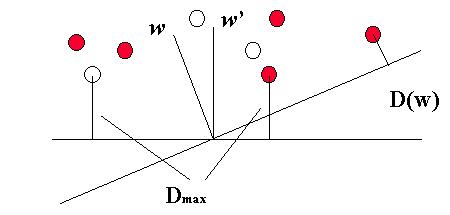
La mejor dirección
para w se obtiene maximizando D(w), lo que determina la solución
óptima del Perceptrón al problema (w ® w’).
![]()
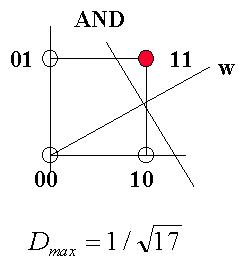
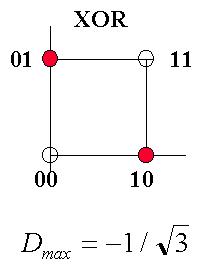
El problema será más fácil a medida que Dmáx sea mayor. En caso de que Dmáx < 0, el problema no puede resolverse con el Perceptrón. A continuación un par de ejemplos:
Perceptrón con UU. P. en Competencia
Una variante interesante y útil para el Perceptrón se obtiene cuando se considera que las UU. P. individuales no son independientes, sino que más bien mantienen una competencia mutua en la tarea de responder correctamente al estímulo de entrada. En este caso la salida del dispositivo se define:

El aprendizaje se
ejecuta cada vez que el elemento de índice k con sk = 1
difiera de la clasificación correcta. En este caso se modifican los vectores de
peso de ambos elementos (ganador k y correcto j), según la regla: