Clase 3

MODELOS BÁSICOS DE COMPUTACIÓN NEURONAL (SEGUNDA PARTE)

· El ADALINE (Adaptive Linear Element, en Inglés)

· Función de Costo y Aprendizaje en el ADALINE

· Comentarios sobre la Regla de Aprendizaje del ADALINE

· Solución Explícita para la Función de Transferencia Lineal

· Alternativa para la Solución Explícita del ADALINE Lineal

· Pesos Sinápticos como Solución de un Sistema de Ecuaciones Lineales

· Convergencia del Descenso de Gradiente como Regla de Entrenamiento

· Otras Funciones de Costo

· Unidad Estocástica de Procesamiento (U. P. Estocástica)

· Dinámica de la U. P. Estocástica

· Regla de Aprendizaje y Optimización del Error

El ADALINE (Adaptive Linear Element, en Inglés)

Es un dispositivo relacional de una sola capa, que es capaz de “aprender” ciertas correlaciones entrada‑salida. Su arquitectura es análoga a la del Perceptrón: difiere sólo en el uso de otras funciones de transferencia. El cómputo que ejecuta el ADALINE es el siguiente:

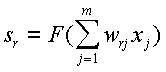
Al igual que en el Perceptrón, s_r es la salida de la U. P., x_i es la componente i‑ésima del patrón de entradas y w_ri es el peso sináptico correspondiente a la i‑ésima entrada de la r‑ésima U. P. En este caso, F(·) es una función de transferencia continua y diferenciable (típicamente, una función sigmoidea, sigmoidea bipolar o la función lineal).

Una ventaja de este dispositivo es que permite la definición de una función de costo que mida la calidad de ejecución (error). Esta función E(W) es diferenciable con respecto a los pesos sinápticos W. De esta forma, puede utilizarse una técnica de optimización, como el descenso de gradiente, para mejorar la ejecución del dispositivo (minimizar el error). De la aplicación del descenso de gradiente se deriva su regla de aprendizaje.

En general, se emplea un método iterativo que permite determinar un conjunto de pesos sinápticos adecuados de manera progresiva, a partir de pesos iniciales arbitrarios.

Función de Costo y Aprendizaje en el ADALINE

Típicamente, se emplea como función de costo, E(W), la suma de los cuadrados de los errores que comete el dispositivo, sobre todos los patrones de entrenamiento z:

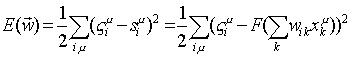
La función E(W) es positiva definida y sólo depende de los pesos sinápticos y de los patrones entrada‑salida. Esta función tiende a cero cuando los pesos se hacen "mejores"; es decir, cuando el dispositivo es capaz de aproximar la relación entrada‑salida.

Dada la función de costo E(W) (superficie en el espacio de pesos), se pueden mejorar los pesos sinápticos W, a través de una dinámica de actualización (cambio) de los pesos que provoque una disminución en el costo E(W).

Una dinámica de este tipo la proporciona el descenso de gradiente:

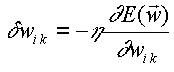
Por lo tanto,

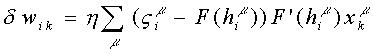
La regla de aprendizaje resultante corresponde al caso de entrenamiento por lote. Este resultado se puede adaptar a la situación de entrenamiento patrón a patrón, escribiendo de nuevo la regla de aprendizaje de la siguiente forma:

donde:

Esta forma es la que se conoce en la literatura como regla delta o de Widrow‑Hoff o regla LMS (de Least Mean Squares, en inglés). Es de notar la presencia de la derivada de la función de transferencia, en contraste a la regla del Perceptrón.

Comentarios sobre la Regla de Aprendizaje del ADALINE

Es fácil ver que el resultado anterior es idéntico a la regla del Perceptrón, en el caso de una función de transferencia lineal. No obstante, las motivaciones de ambas reglas no son las mismas: en el caso presente se busca minimizar la función de costo de funcionamiento del dispositivo, mientras que en el caso anterior se persigue la determinación de un hiperplano separador entre dos clases. Además, las condiciones para la existencia de soluciones son diferentes en ambos casos: separabilidad lineal frente a independencia lineal.

La regla de aprendizaje del Perceptrón converge, en el caso de existir solución, luego de un numero finito de iteraciones. Por su parte, la regla delta es de convergencia asintótica, en principio, luego de muchas iteraciones.

El empleo de diferentes funciones de transferencia sobre el mismo conjunto de entrenamiento, trae como consecuencia que la dinámica de aprendizaje tienda a resultados distintos para los pesos sinápticos.

El enfoque de descenso de gradiente es fácilmente generalizable a redes de varias capas, mientras que la regla del Perceptrón no lo es.

Solución explícita para función de transferencia lineal

En un dispositivo lineal los pesos sinápticos pueden calcularse explícitamente, utilizando el método de la matriz pseudoinversa.

Sea

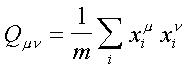
la matriz de “superposición" (overlap, en inglés) de dimensión p ´ p, donde p denota la cantidad de patrones de entrenamiento (se supone que p < m).

Si la matriz Q no es singular, condición que se cumple cuando los patrones de entrada son linealmente independientes, podemos definir la matriz de pesos:

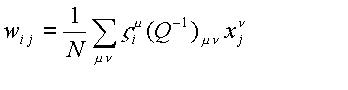
El que esta relación define los pesos correctos, es fácilmente verificable:

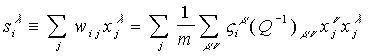
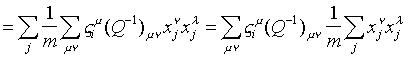
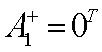
La formulación anterior también puede concebirse, redefiniendo el conjunto de patrones de entrada así:

Lo cual implica la siguiente propiedad:

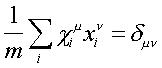
En esta relación es donde se aprecia el concepto de pseudoinversa. Si se considera c y x como matrices, entonces puede escribirse:

donde la matriz:

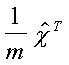
se denomina la pseudoinversa de la matriz x.

De manera más general, para cualquier matriz M de dimensión m ´ n, con m ³ n, la pseudoinversa generalizada o inversa de Moore‑Penrose puede definirse como:

siempre y cuando exista la inversa:

Obviamente,

sin que la relación necesariamente sea conmutativa.

Alternativa para la Solución Explícita del ADALINE Lineal

Una alternativa para la matriz de pesos sinápticos puede obtenerse en términos de la expresión:

de la forma:

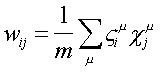
Esta expresión establece que la matriz de pesos es la suma de productos externos de los vectores c y z:

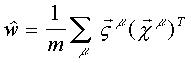
La matriz w transforma los patrones de entrada x en los patrones de salida z:

Por lo que entonces, la matriz w obtenida con la pseudoinversa constituye un proyector en el subespacio m‑dimensional de patrones, y cualquier vector en este subespacio es estable bajo la aplicación de la matriz w. Por esta razón, esta metodología suele denominarse el método de proyección.

Pesos Sinápticos como Solución de un Sistema de Ecuaciones Lineales

La ecuación anterior sugiere que el problema de la determinación de la matriz m ´ n de pesos sinápticos en el ADALINE lineal puede concebirse como la resolución de un sistema de ecuaciones lineales.

Dados los p patrones x y z, si p < m, existen muchas soluciones diferentes para este sistema. La solución que se obtiene con la pseudoinversa es la única que cumple que, para cualquier vector y ortogonal al espacio de los patrones x, se verifica:

Es fácil darse cuenta de que la matriz Q de superposición no es invertible, si existe alguna dependencia lineal entre los patrones de entrada. El resultado general es entonces:

El ADALINE Lineal resuelve el cómputo de sintetizar la relación entrada‑salida, para patrones de entrada linealmente independientes.

Tal condición es suficiente, pero no necesaria, ya que es posible determinar soluciones por otros métodos.

Un conjunto de p patrones de entrada es linealmente independiente, sólo si p £ m, por lo que el número máximo de asociaciones arbitrarias almacenables es m.

Si existe dependencia lineal, la solución que el método determina no es única, ya que los patrones sólo generan un subespacio del espacio de entrada.

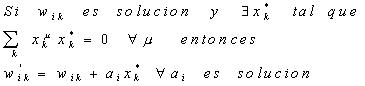
Convergencia del Descenso de Gradiente como Regla de Entrenamiento

Hemos supuesto que la función de calidad que se optimiza en el entrenamiento por el método de descenso de gradiente es cuadrática en los pesos sinápticos:

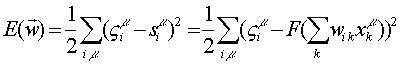
por lo que, en el subespacio de los patrones, conforma una superficie en forma de un paraboloide con un sólo mínimo, el cual toma un valor de cero, si los patrones son linealmente independientes.

En dirección ortogonal a todos los patrones, el error es constante, en virtud de la discusión anterior:

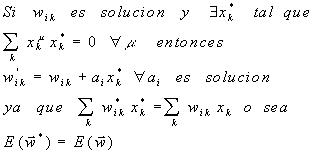
Esto significa que la superficie de error en el espacio de patrones o pesos es como una canal:

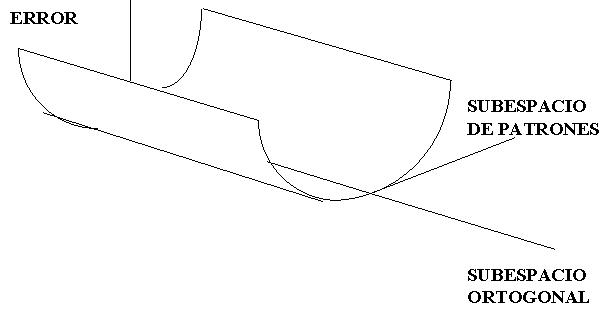
La regla de descenso de gradiente produce cambios en w, sólo en la dirección de los vectores patrón, por lo que cualquier componente de w ortogonal a ellos permanece constante.

La regla necesariamente disminuye el error, si la constante de aprendizaje es suficientemente pequeña. De este modo, con suficientes iteraciones siempre se alcanza el fondo del valle o se llega arbitrariamente cerca.

Otras Funciones de Costo

La expresión de mínimos cuadrados no es la única posibilidad. En principio, cualquier función de las salidas del dispositivo s y de las salidas deseadas z que presente un mínimo cuando éstas sean iguales puede emplearse.

Para cualquiera de estas escogencias, la regla de descenso de gradiente provee una estrategia para la determinación de los pesos sinápticos:

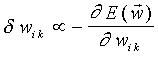
Una alternativa que ha recibido bastante atención es:

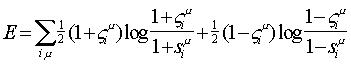
Su interpretación es natural, en términos del aprendizaje de las probabilidades correctas de un conjunto de hipótesis representadas por las unidades de salida:

es la probabilidad de que la hipótesis representada por la i‑ésima U. P. sea verdadera.

se interpreta como probabilidad objetivo.

es certeza.

es falsedad.

Esta función de costo es siempre positiva, excepto cuando s = z, para todo i y m, en cuyo caso se anula. Su ventaja con respecto a la medida cuadrática estriba en que diverge, si la salida de alguna unidad se satura en el extremo incorrecto. Esto contrasta con la tendencia a una constante de aquélla, lo que trae como consecuencia que la dinámica de aprendizaje conduzca hacia una “meseta” relativamente plana de E durante largo tiempo.

La medida de entropía relativa arroja buenos resultados en ciertos problemas en los cuales la energía cuadrática no lo hace.

También resulta conveniente, si los datos de entrenamiento son probabilísticos o difusos (como, por ejemplo, en la asociación de síntomas con sus causas, en el diagnóstico médico).

Calculando el gradiente de E, suponiendo una función de transferencia F(x) = tangh(x), la regla de ajuste de pesos resultante es:

la misma expresión que en el caso del ADALINE lineal o del Perceptrón.

Unidad Estocástica de Procesamiento (U. P. Estocástica)

Una generalización interesante del dispositivo adaptativo lineal es el considerar unidades de proceso estocásticas. En este caso, el cómputo de la unidad se define probabilísticamente:

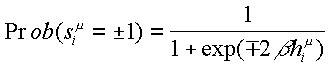
donde el potencial presináptico es:

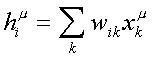
En la expresión anterior, b representa un parámetro que determinará el grado de estocasticidad de la U. P.

La justificación biológica detrás de esta generalización está en que las neuronas observan cierto comportamiento errático: se activan con diversa intensidad; se producen retardos en las sinapsis; existen fluctuaciones aleatorias en la emisión de neurotransmisores, los cuales, a su vez, se difunden estocásticamente a los neuroreceptores; etc. Tal cúmulo de efectos podría modelarse como “ruido” y representarse crudamente como una suerte de fluctuaciones térmicas de la U. P.

El parámetro b se utiliza como una pseudotemperatura que controla el nivel de ruido o el grado de desviación de la U. P. de su comportamiento determinista. Este parámetro suele definirse como:

donde: T es la pseudotemperatura en cuestión.

El efecto del parámetro b puede entenderse, si se considera su influencia sobre la distribución de probabilidad, expresada en términos de una función sigmoidea:

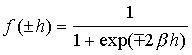
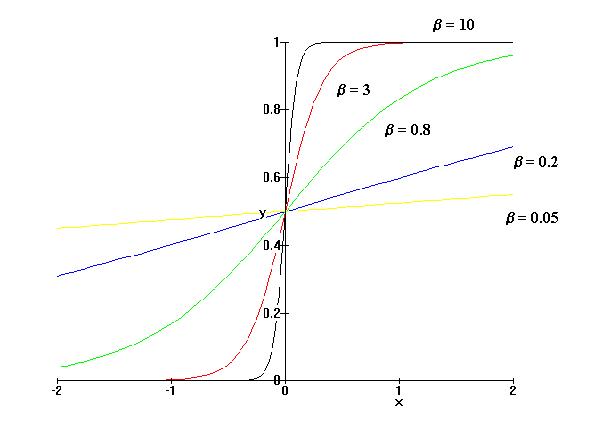
En esta gráfica observamos cómo la distribución de probabilidad tiende al comportamiento determinista, a medida que el parámetro b se hace más grande (bajas pseudotemperaturas T y, por ende, poco ruido térmico). Por otra parte, para b pequeños (grandes pseudotemperaturas T) la distribución tiende a un valor constante de ½, correspondiente a una situación de elevado ruido térmico.

Dinámica de la U. P. Estocástica

La distribución de probabilidad para la actividad de la U. P., la cual establece su dinámica estocástica, determina que el valor esperado para la salida <s> del dispositivo viene dado por:

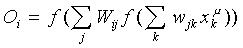
Esta expresión puede utilizarse en las simulaciones para calcular el valor esperado de las salidas. No obstante, en redes estocásticas reales, el valor esperado se obtiene promediando las salidas de las U. P. sorteadas en cada iteración, de acuerdo con la probabilidad expuesta, durante un número adecuado de actualizaciones.

Regla de Aprendizaje y Optimización del Error

El valor esperado es la base de la ley de aprendizaje que toma la forma:

con

lo cual es una suerte de regla delta promedio.

Es interesante verificar que esta regla de aprendizaje siempre disminuye el error promedio en la medida cuadrática:

Bajo la suposición de que los patrones de salida son bipolares, la medida anterior puede escribirse de nuevo como:

Por lo que el error promedio en la U. P. estocástica es:

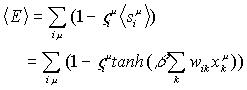
Para determinar el cambio en <E> en un ciclo de corrección de pesos, debemos calcular la variación D<E> con respecto a los pesos:

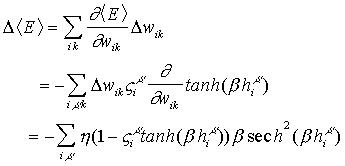
Como puede apreciarse en este resultado, la expresión para la variación del error promedio con respecto a los pesos sinápticos es, obviamente, siempre negativa, de tal forma que el procedimiento de corrección de pesos siempre mejora el desempeño promedio del dispositivo.