Fig
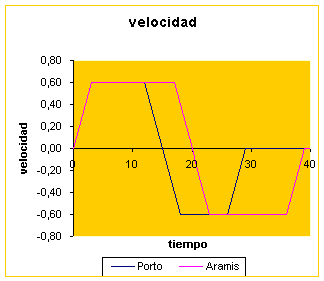
1a. Velocidad en unidades de C (velocidad de la luz) en función del
tiempo para los dos viajeros, la aceleración es la pendiente a esta gráfica.
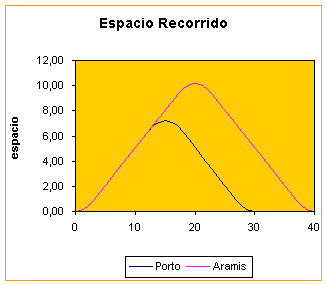
Fig.1b.
Espacio recorrido, en años luz, por los dos viajeros.
| La Paradoja de los
Gemelos
|
||||
|
En los libros de Física General, en la sección dedicada a la Relatividad, se suele discutir el resultado paradójico en la edad de dos gemelos; uno que se mantiene en Tierra y el otro que viaja a un planeta situado más allá de nuestro sistema solar, y que, al regreso, se encuentra más joven que el gemelo que permaneció en Tierra.
La paradoja consiste en el hecho de que sí bien un gemelo ve al segundo viajando a cierta velocidad, simétricamente, desde el punto de vista del segundo gemelo, es el primero el que se mueve respecto a él. La explicación a la paradoja es que esta simetría no es tal, puesto que el gemelo viajero ha estado sometido a aceleraciones, mientras que el gemelo más viejo no ha sido sometido a aceleraciones.
Esta explicación, que se encuentra en estos manuales, induce a pensar que la aceleración actúa de algún modo para que el tiempo pase más lentamente en los sistemas acelerados. Lo cual es falso, como ilustraremos a continuación.
Para ello consideremos tres trigéminos:
Athos, Portos y Aramìs. Athos permanece en Tierra mientras Portos y Aramìs
viajan a planetas lejanos y luego regresan a Tierra. Desde el sistema de
referencia de Athos, fijo a Tierra, Portos viaja 3 años con aceleración
constante hasta alcanzar una velocidad de 0.6 C, C es la velocidad de la luz.
Sigue con esta velocidad 9 años más y luego cambia la dirección de su
velocidad con aceleración constante hasta invertir su velocidad en los 6 años
consecutivos. Viaja 9 años de regreso y luego desacelera hasta quedar en reposo
en el sistema Tierra donde se encuentra Athos y después de 10 años de espera
regresa también el tercer gemelo Aramìs,
|
|
|
|
Fig
1a. Velocidad en unidades de C (velocidad de la luz) en función del
tiempo para los dos viajeros, la aceleración es la pendiente a esta gráfica. |
Fig.1b.
Espacio recorrido, en años luz, por los dos viajeros. |
.
Aramìs, lo mismo que Portos, acelera 3 años consecutivos hasta alcanzar la velocidad de 0.6 C. Luego mantiene esta velocidad por 14 años en vez de nueve, y regresa a Tierra, invirtiendo la velocidad, que mantiene otros 14 años; y luego desacelera tal cual lo hizo Portos, para al fin conseguirse los tres gemelos en Tierra.
En la figura observamos los gráficos de velocidad y espacio recorrido en función del tiempo para los dos viajeros en el sistema de referencia de Athos.
Tanto Portos como Aramìs han estado sometidos a aceleraciones iguales durante tiempos iguales, aunque no simultáneamente.
Para limitarnos a un nivel elemental no calcularemos el tiempo propio de los viajeros durante el tiempo que estuvieron acelerados (tiempo propio = tiempo transcurrido, medido por un reloj en el sistema). Basta notar que el tiempo transcurrido mientras abandonaban Tierra para alcanzar una velocidad de 0.6 C es un tiempo igual para los dos y lo denotaremos t1 , En cuanto al pasaje de la velocidad 0.6C a –0.6C El tiempo propio de Portos debe ser igual al tiempo propio de Aramìs cuando él haga la operación de cambio de dirección de su velocidad, puesto que ambos pasan de una velocidad de 0.6 C a –0.6C con aceleración constante en 6 años medidos en el sistema de Athos, este tiempo lo podemos denotar t2 , por último, al fin de su viaje, los dos desaceleran con aceleración constante pasando de velocidad –0.6C a cero en tres años, denotaremos este tiempo t3 .
El tiempo de cada viajero será la suma t1 + t2 + t3 + el tiempo propio durante el cual viajaron a velocidad constante, para Porto agregaremos los 10 años de espera. Estos pueden calcularse a partir del tiempo medido por Athos por medio de las transformaciones de Lorentz.
El tiempo de Portos será ![]() +
10 años de espera = 24.4
+
10 años de espera = 24.4
El tiempo de Aramìs será ![]() =
22.4
=
22.4
Aramìs será por lo tanto más joven que Portos en dos años.
De este modo hemos ilustrado como la aceleración no es determinante en el comportamiento del tiempo propio de un sistema.
No es fácil dar una explicación intuitiva a los resultados de la relatividad. Debe ésta comprenderse a través del estudio de ejemplos, hasta resolver todos los elementos que nos confunden.