volver a p�gina principal.
EL SOFISMA Y LA PARADOJA EN LA ENSEÑANZA DE LA
FÍSICA.
Renato Iraldi
1.- Introducci�n.
Paradojas y sofismas representan rompecabezas cuya soluci�n nos
ayuda a desarrollar la intuici�n mas que cualquier otra aplicaci�n. Un sofisma
es un razonamiento que nos parece irreprochable pero que, sin embargo, contiene
un error que nos lleva a un resultado que al final nos resulta absurdo o que
contradice principios fundamentales. Una paradoja, en cambio, representa una
deducci�n cuyo resultado nos parece una insensatez o una contradicci�n pero que,
en realidad, este resultado es correcto o si hay una contradicci�n esta
contradicci�n proviene de un sofisma.
Paradojas y sofismas est�n estrechamente relacionadas, las dos representan una contradicci�n entre un
resultado correcto y un resultado o una convicci�n incorrecta.
La contradicci�n puede provenir de tres fuentes principales:
- Un impedimento
psicol�gico para abstraerse de la realidad y adoptar una posici�n ideal; como
ejemplo de este tipo podemos citar la paradoja de la inercia, la ley de inercia
nos parece contradictoria puesto que la experiencia diaria nos indica que, todos
los cuerpos en movimiento, o lo pierden o tienen un motor que lo mantiene.
- Una convicci�n del sometimiento de la naturaleza a ciertas reglas fundamentales,
como por ejemplo la naturaleza absoluta del tiempo, que nos lleva a la paradoja
de los gemelos en relatividad. O la convicci�n de que el futuro de una
determinada situaci�n f�sica debe estar predeterminado. � Dios no puede jugar a
los dados� que nos conduce a la paradoja de Einstein, Podolski y Rosen.
- Un sofisma que conduce a un resultado que contiene una contradicci�n con principios
bien establecidos.
Estos sofismas en general se basan en el descuido de una
propiedad que juega un papel fundamental y no se toma en cuenta. La paradoja
hidrost�tica es un ejemplo de este caso. La paradoja hidrost�tica fue planteada
por primera vez por Stevin (1548 -1620): Observa, �ste, que el peso del l�quido
contenido en un recipiente puede ser diferente a la fuerza debida a la presi�n
del l�quido sobre el fondo del recipiente. Ver fig.1
 |
|
Fig. 1 Tres recipientes cuyos fondos tienen
igual �rea A y contienen agua hasta la misma altura h. Si comparamos los
pesos encontramos Pa> Pb> Pc . Sin embargo, la fuerza que ejerce el
l�quido sobre el fondo del recipiente es id�ntico en
los tres casos. |
Esta paradoja se hace presente si descuidamos las fuerzas que el l�quido
ejerce sobre las paredes del recipiente, en el caso de que las paredes no sean
verticales una componente de la fuerza sobre estas paredes contribuye en la
formaci�n del peso.
(Ver Fig 2.)
 |
|
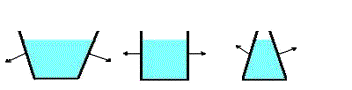
Fig 2. La presi�n y las �reas del fondo
para los tres recipientes es la misma, por lo que las fuerzas en los
fondos de los recipientes F= P A son iguales, pero el peso de los tres
vol�menes de l�quidos son diferentes, porque hay que tomar en cuenta
tambi�n la fuerza sobre las paredes laterales. En el primer caso las
fuerzas sobre las paredes laterales contribuyen al peso al igual que las
fuerzas sobre el fondo, en el segundo caso no hay contribuci�n y en el
tercer caso las fuerzas sobre las paredes laterales contribuyen
negativamente al peso. |
La resoluci�n de estos rompecabezas no es una tarea
intranscendente, es el mejor ejercicio intelectual para poder escapar de la
superficialidad y de la sumisi�n a los c�nones establecidos, y nos sirve para
descubrir los peque�os malentendidos que son compartidos por la enorme mayor�a
de los estudiantes de los primeros a�os de licenciatura.
2. Planteamiento del problema.
En este trabajo presentamos un sofisma que nos conduce a una
violaci�n del principio de conservaci�n de la energ�a.
Consideremos un tubo
cil�ndrico compuesto de dos secciones de �reas A1 y
A2 Este tubo contiene dos pistones
conectados por una barra inextensible, Ver fig. 3. Los pistones pueden
deslizarse sin fricci�n en el tubo. Los tubos est�n abiertos a la atm�sfera
mientras que en la parte interior a los dos pistones hay un gas ideal a
temperatura T0 y a una presi�n p
mayor que la atmosf�rica lo que le permite soportar el peso de un cuerpo que
descansa sobre el pist�n en la parte inferior del tubo; como muestra la
figura 3.
 |
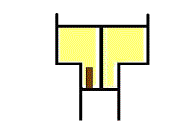Fig 3. Un aumento en la temperatura del gas
interior debe producir un aumento en el volumen del gas para mantener la
misma presi�n p y preservar el equilibrio mec�nico.
|
La presi�n en el interior del cilindro no puede cambiar puesto que
una presi�n mayor producir�a un rompimiento del equilibrio mec�nico al producir
una fuerza sobre el pist�n superior mayor que la ejercida sobre el pist�n
inferior por la presi�n y el peso de la carga colocada sobre �l. Si la presi�n
tendiera a aumentar los pistones se desplazar�an hacia arriba aumentando el
volumen para mantener la presi�n constante. Si el gas encerrado aumenta su
temperatura, por la inyecci�n de calor, deber�n elevarse los pistones para
mantener la misma presi�n y el equilibrio mec�nico,. Calculemos la altura que
recorrer�n los pistones si el aumento de temperatura es DT
Como la presi�n debe quedar igual
para preservar el equilibrio mec�nico y la cantidad de gas encerrado no cambia.
Entonces:
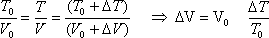
La variaci�n del volumen la logra
el sistema al subir los pistones una altura h, pues:
DV=(A1-A2)h
igualando estas dos ecuaciones
tenemos el resultado buscado:
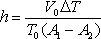
Podemos analizar este resultado,
en particular las condiciones l�mites para evaluar la plausibilidad de la
soluci�n, tanto para convencernos de que el resultado no es contradictorio como
para ganar intuici�n sobre el sistema en estudio. Muchas veces este
procedimiento nos permite detectar errores, sea de procedimiento como de errores
de concepci�n.
Comparemos la energ�a potencial ganada por el cuerpo que
descansa sobre el pist�n al inyectar una determinada cantidad de calor DQ, este calor puede suministrarse, por ejemplo, prendiendo
un f�sforo en el interior del tubo. Para el ejemplo que tratamos:
DQ=Cp
DT
Donde Cp es el calor espec�fico a presi�n constante del
gas interior. Podemos entonces escribir:
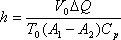
Correspondiendo a un aumento de
energ�a potencial de la carga de:
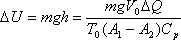
Con una determinada cantidad de
calor DQ inyectado al sistema podemos escoger la
diferencia en �reas A1- A2 arbitrariamente peque�a y obtener cualquier
cantidad de energ�a potencial que queramos. Esto no est� en acuerdo con la
conservaci�n de la energ�a. �Como podemos explicar esta aparente contradicci�n?
3. Resoluci�n
del sofisma.
Primeramente calculemos la
presi�n p en el interior del tubo. Para preservar el equilibrio mec�nico,
dada una determinada temperatura, tenemos:
mg=(p-pa)A1+(pa-p)A2=p(A1-A2)=p(A1-A2)-pa(A1-A2);
pa = presi�n atmosf�rica.
por lo que la presi�n en la parte
interior a los pistones es:
p=pa+mg/(A1-A2)
Vemos que tambi�n la presi�n en el
interior del tubo debe tender al infinito cuando las �reas de los pistones se
igualan.
Ahora bien, para un gas ideal:
Cp=5/2 nR
con n= n�mero de moles
y R la constante universal de los gases. La ley de los gases pV = n R
T nos dice que: n=pV/RT. Sustituyendo en la expresi�n de la energ�a
potencial con el valor dado de n tenemos:
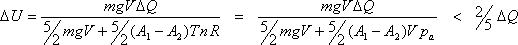
Por lo tanto la transformaci�n de calor en potencial no puede tener una
eficiencia mayor a 2/5 y no se viola el principio de conservaci�n de la energ�a.
Referencias.
1. Paradojas y sofismas f�sicos. V.
Langue; Editorial Mir, Moscu 1978
Renato Iraldi. http://fisica.ciens.ucv.ve/
Douglas Figueroa.
Volver
al principio