La paradoja de Einstein Podolski y Rosen[1] (E.P.R) ha constituido un reto a las creencias de la mayoría de los físicos, pues toca una de las suposiciones básicas de todo trabajo científico: La predecibilidad. La creencia de la mayoría de los físicos es que la naturaleza tiene que ser estrictamente causal; los sucesos al azar, como por ejemplo: el lanzamiento de dados, cuyo resultado no es predecible, se debe a una ignorancia momentánea de los datos iniciales y a una imposibilidad de tomar en cuenta, en las ecuaciones descriptivas, todos los factores implicados en las ecuaciones de evolución y no a una propiedad intrínseca de la naturaleza. Esta creencia ha conducido a algunos físicos a afirmar que la mecánica cuántica debe considerarse como una formulación estadística de una teoría mas fundamental; la incertidumbre cuántica debería, según esta interpretación, ser considerada de la misma clase de incertidumbre que se presenta en la formulación de la mecánica estadística.
La paradoja E.P.R, precisamente, apunta en esa dirección, tratando de mostrar que la incertidumbre cuántica no es intrínseca a la naturaleza. La publicación de ese trabajo abrió las puertas a una avalancha de artículos, unos defendiendo la interpretación de la naturaleza intrínseca de la incertidumbre cuántica (interpretación de Copenhagen) y otros tratando de establecer una teoría mas fundamental cuyo tratamiento estadístico conformaría la mecánica cuántica (teorías de los parámetros ocultos)
2.- Correlaciones
Consideremos un conjunto de espines 1/2 todos preparados en el mismo estado cuántico |z,+> y avanzando hacia un medidor de la componente z del espin. En este caso podemos predecir con absoluta precisión el resultado de las mediciones, este resultado será una serie de + 1/2 que denotaremos S.
S ={ +,+,+,+,…}
En cambio, si los electrones se acercan a un medidor de la componente x del espin el resultado de las mediciones será una serie de + y - totalmente al azar. Si medimos en una dirección muy cercana al eje z obtendremos una serie de + y - pero con una probabilidad grande de obtener + y una probabilidad pequeña de obtener -.Definimos el coeficiente de correlación entre dos series de medidas como:
h = P++ + P-- + P+ - +
P-+
donde P++ es la probabilidad de que si el n-esimo signo de la primera serie es + entonces el n-esimo de la segunda serie sea +, y definiciones equivalentes para los otros símbolos.
Supongamos ahora que tenemos dos conjuntos de espines todos preparados en el mismo estado |z,+>, si los dos conjuntos se miden según el eje +z, obtendremos dos series que contendrán todos signos +, y el coeficiente de correlación será h=1.
Si un conjunto de espines se mide en la dirección +z. y el segundo conjunto en la dirección +x entonces obtendremos dos series: una serie de signos + y una serie de signos + y - al azar. En este caso: P++ = P+ - = 1/2, y el coeficiente de correlación será cero. Si medimos el primer conjunto según el eje +z y el segundo según el eje que forma un ángulo q con el eje z , vamos a tener dos series S{1} y S{2} con correlación:
Supongamos que tenemos un conjunto de pares de partículas de espin ½ cuyos estados de dos partículas tengan un momento angular total J = 0, y que llamaremos pares E.P.R. Si dirigimos los pares de partículas a detectores diferentes A y B, como en la Fig.1, estos pares estarán fuertemente correlacionados. (Note que los ejes en A se escogen dirigidos en dirección contraria a los ejes en B, si el eje z de A apunta hacia abajo, entonces el eje z de B apunta hacia arriba).
| fig. 1 Pares de electrones se dirigen a dos detectores, A y B. Note que los ejes locales tienen direcciones contrarias en A respecto a las direcciones en B. |
Si, ambos A y B, miden la componente de su eje local +z, entonces la correlación entre las medidas será: hzz =1. En general, si los dos miden la componente de los espines según el mismo eje local, tendremos hzz =1: Si A mide la componente +x y B la componente +z el valor será hzx =0. Mas general, si A mide en la dirección +z y B en la dirección que hace un ángulo q con la dirección +z entonces: hzq = cos q .
4.- Una predicción paradójica.
Consideremos nuevamente el sistema descrito en la fig.1, la mecánica cuántica sólo nos permite predecir las probabilidades de la medición en una dirección para A y una dirección para B; por lo tanto, sólo podremos predecir las correlaciones para una secuencia de medidas en A con otra secuencia de medidas en B, la fig.2 nos muestra el resultado del cálculo, de las correlaciones en el contexto de la mecánica cuántica, entre las medidas posibles sobre este sistema; donde se denota la serie de medidas, de la componente x de los espines, que obtendría A en el conjunto de espines que se dirigen hacia él como Sx(A) y en la misma forma definiremos: Sz(A) y Sq(A) . Y lo mismo para B. i.e
![]()
![]()
![]()
Las correlaciones entre las otras posibles medidas se obtienen, de las dadas, por simetría.
Suposiciones:
Los detectores A y B pueden encontrarse muy alejados uno del otro, y las medidas pueden realizarse simultáneamente, por lo que asumiremos:
1.- Localidad: las medidas efectuadas en B no pueden afectar el resultado de las medidas efectuadas en A, y recíprocamente.
Si subyacente
a la mecánica cuántica existe una descripción por parámetros ocultos,
entonces:
2.-
"Determinismo"[2] Dado un conjunto de electrones acercándose a un
aparato de medida y dado el eje en que se va a realizar la medida, las salidas
están predeterminadas.
Tomando en cuenta estas dos suposiciones tenemos que:
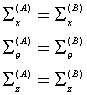
por lo que:
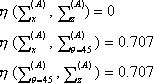
En el apéndice 4 se demuestra que: Si tenemos dos series de salidas +,- al azar y cuya correlación es =0, y otra serie de salidas + y - al azar cuyas correlaciones con las dos primeras valen: h1 y h2 entonces:
h1 + h2 £ 1
Este teorema es un caso particular de un teorema mas general que se debe a Bell[3]. Las ecuaciones de arriba violan, claramente, esta última desigualdad. Debemos concluir, por lo tanto, que:
O bien la mecánica cuántica no se adecúa a la descripción de los espines, o bien una de las suposiciones 1 o 2 es falsa.
La mecánica cuántica no puede falsificarse por este medio porque las correlaciones dadas por la fig.2 han sido confirmadas experimentalmente. Por lo tanto, una de las suposiciones debe ser inadecuada para la descripción de los sistemas que se estudian en la física.
La violación de la suposición 2, la falta de determinación, es algo que los físicos se niegan a considerar. Esto se puede ilustrar con la célebre frase de Einstein "Dios no juega con los dados".
La otra posibilidad es que la medida simultánea de un detector (B) pueda afectar simultaneamente a otro detector (A) situado a gran distancia; en este caso admitiríamos la posibilidad de que la información viaje a velocidades superlumínicas y se trastorne la relación causa-efecto. Sin embargo, esta información que se transmitiría a velocidad superlumínica sólo sirve para darle una interpretación determinista a la mecánica cuántica pero no nos serviría para la transmisión de una verdadera información.
4.- Conclusiones.
En este trabajo he tratado de presentar en forma elemental, accesible a estudiantes de la licenciatura, uno de los dos grandes problemas de la teoría de la medida en mecánica cuántica. La violación, por parte de los postulados de la medición, de las desigualdades de Bell, y, por lo tanto, la imposibilidad de formular una teoría de parámetros ocultos local (consistente con la relatividad) y determinista (predictiva). La falta de cualquiera de estas propiedades le quitaría toda utilidad a una teoría de parámetros ocultos.
[1] A. Einstein, B.Podolsky and N. Rosen. Phys Rev. 47 (1935) 777
[2] J. S. Bell, Physics (N.Y) 1, 195, (1965)
[3] A. Aspect, P. Grangier and G. Roger. 49, 2 (1982) 91
Renato Iraldi Riraldi@yahoo.com
Apéndice
Definiciones:
Serie de mediciones, es una serie de signos + o - al azar, provenientes de la medición de la componente del espín según un eje dado.
Correlación entre dos series de medidas.- Definiremos la correlación entre dos series de medidas como:
h = P+ + + P- - - P+ - - P-
+
donde P+ - es la probabilidad de que el enésimo signo de la primera serie es + y el enésimo de la segunda serie - . Y definiciones similares para los otros símbolos.
Sea P+ + + La probabilidad de que el enésimo signo de la primera serie sea + , el enésimo de la segunda sea + y el enésimo de la tercera + .
Teorema (Bell): Si tenemos dos series de medidas con salidas + y - al azar, cuya correlación sea h(1,2) = 0, y una tercera serie de medidas cuya correlación con las dos primeras sea h(1,3) y h(2,3) Entonces:
h(1,3) + h(2,3) £ 1
Demostración.- Sea
h(1,3) = P+
+(1,3) + P- - (1,3) - P+ -(1,3) - P- +(1,3)
h(2,3) = P+ +(2,3) + P- - (2,3) - P+ -(2,3) - P- +(2,3)
Para todas las series P+ + P- = 1 la correlación entre las series de medidas también puede escribirse: Usando expresiones del tipo P+ + = P+ + (P+ + P-) = P+ + + + P+ + - . donde se sobrentienden los superíndices 1,2,3
h(1,3) = P+ + +
+ P+ -+ + P- + - + P- - - - P+ +
- - P+ - - - P- + + - P- -+
h(2,3) = P+ + + + P-
+ + + P+ - - + P- - - - P+ + - - P- +
- - P+ - + -
P- - +
Sumando tenemos:
h(1,3) + h(2,3) =2 P+ + + + 2 P- - - -2 P+ + - -2 P- - +
usando:
P+ +.+ = P+ +(1,2) - P+ + - y P- - - = P- - (1,2) - P- - +
queda:
h(1,3) + h(2,3) = 2 P+ +(1,2)
+ 2P- -(1,2) - 4P+ + - - 4P- -
+-
como h(1,2) = 0 = P+ +(1,2) + P- - (1,2) - P+ -(1,2) - P- +(1,2) = 0
y P+ +(1,2) + P- - (1,2) + P+ -(1,2) + P- +(1,2) =1
sumando tenemos:
2P+ +(1,2) + 2 P- - (1,2) = 1, y
h(1,3) + h(2,3) = 1- 4P+ + - -
4P- - +
£ 1
Q.E.D