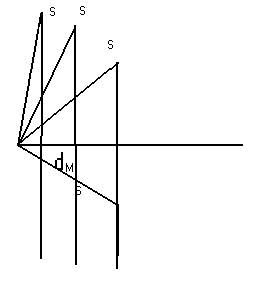
Fig.1. Las supuestas
trayectorias, seg�n Arist�teles. El m�vil se mueve una distancia dM en la
direcci�n que fue lanzado y luego cae verticalmente.
Lanzamiento de proyectiles.- Teor�a Aristot�lica.
Renato Iraldi
La especulaci�n cient�fica comienza en Grecia en el siglo VI a.C. y llega a su punto m�s prominente en las mentes esclarecidas de Plat�n y Arist�teles. Plat�n sosten�a que el mundo f�sico debe entenderse s�lo a partir de la raz�n, para Plat�n la ciencia debe derivarse de la teolog�a. Arist�teles a�n siendo un plat�nico de joven, pronto se aparta de su maestro y establece una filosof�a alternativa. Su trabajo, predominantemente en biolog�a, lo conduce a desarrollar el m�todo de investigaci�n que denominamos el m�todo emp�rico. Este m�todo consiste en buscar, por la observaci�n, algunas verdades indubitables y a partir de ellas, con reglas l�gicas tambi�n establecidas por �l (L�gica Aristot�lica), deducir y explicar los fen�menos naturales.
El m�todo Aristot�lico aplicado al estudio del movimiento nos encara a la pregunta de cuales son sus causas, puesto que nunca observamos que los cuerpos conserven el movimiento o que un cuerpo en reposo comience a moverse por s� solo. Por lo tanto, una verdad indubitable es que el movimiento tiene una causa y que al acabarse la causa tambi�n �ste se acaba. Arist�teles reconoc�a dos causas del movimiento: una natural, que pose�an todos los cuerpos pesados, y consist�a en la necesidad de buscar su posici�n natural, que es la de estar lo m�s cercano posible al centro de la Tierra. Seg�n Arist�teles las piedras caen porque �sta es su naturaleza. La otra causa es la que act�a en el movimiento forzado, como cuando se lanza una piedra, en este caso es un motor (el lanzador) el que imprime el movimiento, y el m�vil conserva una parte que se va desgastando por la acci�n de la resistencia del aire; Pero Arist�teles supon�a que es tambi�n el aire el responsable de seguir empujando al m�vil, jugando as� un doble papel.
Las observaciones aplicadas al estudio de proyectiles conducen a Arist�teles a formular un modelo paradigm�tico para este tipo de m�viles: El proyectil, al ser lanzado, conservar� su movimiento ascendente en l�nea recta hasta consumir su movimiento forzado, recorriendo una distancia S. Luego, desde el punto en que ha llegado, se mover� verticalmente en b�squeda del centro de la Tierra. La trayectoria paradigm�tica se muestra en la fig.1.
|
|
Fig.1. Las supuestas
trayectorias, seg�n Arist�teles. El m�vil se mueve una distancia dM en la
direcci�n que fue lanzado y luego cae verticalmente. |
En la literatura que ha llegado hasta nosotros, de esa �poca, no hay ning�n an�lisis cuantitativo de esta aproximaci�n al estudio del movimiento de proyectiles ni su comparaci�n con el experimento. Lo que s� conocemos es que este modelo fue un�nimemente aceptado por los antiguos y fue usado hasta la edad media. Fue Galileo ( 1564-1642 ) quien muestra que este modelo nos lleva a un callej�n sin salida y formula el que conocemos hoy en d�a. A partir de all� el modelo de Arist�teles s�lo ha recibido cr�ticas destructoras, a tal punto que se ha acusado a todos los griegos de la antig�edad de aceptar verdades sin someterlas a la m�nima prospecci�n experimental, lo que me parece no s�lo exagerado sino totalmente injusto. Galileo vuelve al m�todo Plat�nico de analizar la realidad por medio de la raz�n explorando modelos idealizados, aunque no se puedan observar. Esto le permite formular un modelo paradigm�tico consistente en despreciar al aire y basado en el principio de inercia; tal como hoy lo conocemos. Ya Arist�teles hab�a considerado el movimiento en el vac�o, con reflexiones parecidas a las de Galileo, pero llegando a conclusiones diferentes. �Como el aire se resiste al movimiento de los cuerpos, si el aire fuera sacado, un cuerpo o bien se quedar�a quieto, porque no tendr�a donde ir, o si se mueve se quedar�a moviendo con la misma velocidad para siempre. Como esto es absurdo; no puede existir el vaci�(1).
Como ejercicio acad�mico
podemos analizar hasta donde el modelo Aristot�lico permite hacer predicciones.
Para ello buscaremos una consecuencia de su modelo y la compararemos con el
resultado experimental.
Debemos tomar el modelo en su l�mite paradigm�tico, donde el m�vil al final ha consumido todo el movimiento en la direcci�n horizontal y se mueve verticalmente. Definiremos la distancia m�xima horizontal dM como la distancia horizontal que el proyectil ha recorrido una vez que alcanza la situaci�n en que su velocidad s�lo tiene componente vertical. La figura muestra que en la teor�a Aristot�lica la distancia m�xima horizontal ser� igual a: dM=S cosa , donde a es el �ngulo que forma la l�nea de lanzamiento con la direcci�n horizontal. Puesto que el movimiento forzado es independiente del movimiento vertical la distancia recorrida S es independiente de la direcci�n en que fue lanzado el proyectil(2).
En vez de comparar este resultado con el experimento hemos calculado la dM en el contexto de la teor�a newtoniana tomando en cuenta la resistencia con el aire.
La ecuaci�n de movimiento la escribimos: con V0 la velocidad de lanzamiento del proyectil, V la velocidad instant�nea y a el �ngulo de tiro.
para definir la fuerza de
roce hemos utilizado la velocidad m�xima en ca�da libre vl
mediante la ecuaci�n:Fr=L V2 , por lo tanto tenemos:
L=
mg/ vl2
.
Algunas de las trayectorias calculadas de esta manera se muestran en la figura 2. En esta figura se ha utilizado vl=50 m/s, y V0=100 m/s . En la figura 3 se reporta la distancia horizontal m�xima, calculada con las ecuaciones de arriba, considerando como resultado experimental; y la calculada por la expresi�n: dM=S cosa.
Las figuras 2 y 3 muestran la concordancia de las predicciones del modelo Aristot�lico con el modelo Newtoniano en el l�mite paradigmatico: en el l�mite en que el roce con el aire es la fuerza dominante aplicada al m�vil.
 |
 |
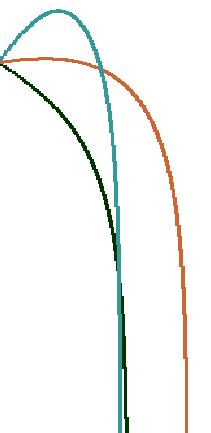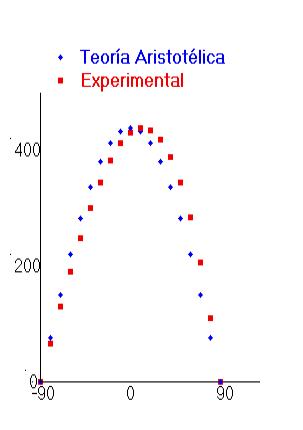| Fig .2 trayectorias de un proyectil en presencia del roce con el aire para tres �ngulos de tiro. Note la gran diferencia que presentan estas trayectorias con una par�bola. | Fig .2 Distancia horizontal m�xima en funci�n del �ngulo de tiro. |
Actualmente consideramos las teor�as cient�fica como si se tratara de verdades absolutas. Esto frecuentemente nos induce a despreciar muchos acercamientos a la verdad cient�fica del pasado present�ndola como una aproximaci�n ingenua y en muchas ocasiones haci�ndole criticas injustas. Con esta muestra pretendo llamar la atenci�n sobre los hermosos trabajos que nos legaron los griegos; dignos de discusi�n en nuestros cursos introductorios de f�sica.
Renato Iraldi. Riraldi@Yahoo.com
Por
modelo paradigm�tico de una
realidad f�sica designamos un modelo en el cual se destacan los efectos m�s
importantes que permiten describir y entender dicha realidad ignorando fen�menos
colaterales, que pueden oscurecer nuestra percepci�n, destacando as� los efectos
esenciales.
Cuando
estudiamos el roce entre dos superficies que resbalan la una sobre la otra
tomamos la fuerza de roce como: F=m N , donde m es un coeficiente que caracteriza a las dos
superficies. Esta ley no es cierta en general s�lo dentro de ciertos l�mites de
la fuerza N es v�lida, adem�s no depende s�lo de los materiales que
conforman las dos superficies, tambi�n depende del grado de pulitura, de la
contaminaci�n, de la temperatura etc. Sin embargo es una ley que se acerca
adecuadamente a la realidad y nos sirve como lugar de partida para incluir otros
efectos. Para esto sirven los modelos paradigm�ticos.
El paradigma Aristot�lico es
adecuado para tratar proyectiles cuyo lanzamiento se realiza a gran velocidad,
donde la fuerza de roce con el aire es predominante frente a la fuerza de
gravedad. La observaci�n de este tipo de movimiento nos da la sensaci�n de una
trayectoria muy parecida a la que propone Arist�teles como paradigma del
movimiento. Sin embargo si observamos lanzamientos a muy baja velocidad entonces
la trayectoria se aleja considerablemente de la trayectoria descrita. Esto
debido a que el m�vil se encuentra sometido a dos fuerzas en competici�n.
Galileo rechaza el paradigma de Arist�teles. �l se plantea el problema de
como debe ser el movimiento en ausencia de aire, una situaci�n imposible en la
�poca, pero mucho m�s cercano a la realidad para movimientos a muy bajas
velocidades donde la resistencia del aire, que es proporcional al cuadrado de la
velocidad, es m�nima(3). Recu�rdese que Galileo estaba interesado en
comprender el movimiento de los p�ndulos, los cuales pasan la mayor parte del
tiempo a velocidades muy cercanas a cero.
El paradigma de Galileo result� mucho m�s �til para entender el
movimiento porque �ste permite agregar en forma matem�tica los otros elementos,
como el roce con el aire, y calcular las trayectorias. As� hoy en d�a aun para
calcular lanzamientos de proyectiles a muy alta velocidad se parte del paradigma
Galileano y, luego, se agregan las fuerzas
de roce, tal como se hace en este art�culo.
(1) ARISTOTLE. Aristotle�s Physics, ed.W.D.Ross, Oxford, 1936
(2) En realidad Arist�teles dec�a que mientras hay movimiento forzado no hay movimiento hacia el centro de la tierra, lo que evidentemente es falso.
(3) En realidad a bajas velocidades la resistencia del aire es proporcional al m�dulo de la velocidad. Pero en ambos casos para velocidades peque�as la fuerza de roce tiende a cero.