III Accelerated translational coordinate system.

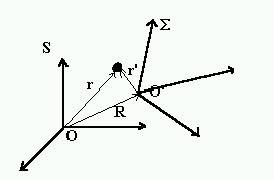
            a) Consider two reference frames S and S’ and a pair of coordinates systems with fixed relative orientations in space. Consider a point P of the physical space, at this location a particule is moving and we will study his movement. The position vector r, of  the particule relative to the origin of the coordinate system S, O (see fig.1), will be denoted ïr>, The position vector R, of the origin O’, of the coordinate system S’relative to the origin O, will be denoted çR>, and the position vector r’, of the particule relative to the origin O’, will be denoted  êr’>. In order to give a algebraic representation of vectors we will take a basis íêe_n>ý in S and a basis íêe_i>ý in S’. From the geometrical point of view we see that

                               êr> = êR> + êr’>                                                                   ...(3)

Fig (1) Moving coordinates systems

Diferentiating this equation we obtain the velocity of the particule relative to O and O’.

çv> = çU> + çv’>           (4)

çv> is the velocity of the particule relative to O and is the velocity measured by an observer fixed in system S, çU> is the velocity of  O’ relative to O; and çv’> the velocity of the particule relative to O’ and is the velocity as seen by an observer fixed in system S’.

If we are interested in the relation between the coordinates of the velocity of the particule as measured by observers in system S and S’, we have to diferentiate equation (4) in the algebraic representation. In order to make this, we have to follow the following procedure: project eq (4) on a coordinate system, diferentiate de coordinates, and, multiply by the unit vectors of this particular coordinate system. This procedure can be sintetized by the application of the operator:

               å₁³ êe_n> d/dt <e_n ê or equivalently  å₁³ êe_i> d/dt <e_i ê

The result of the application of this operator will give eq. (4) in the particular basis used.

In the following, we will assume that repeated indexes will denote sum.

            Time diferentiation of eq.(4) in S gives:

                                êe_n> d/dt <e_nçr> =  êe_n> d/dt <e_nêR> +  êe_n> d/dt <e_nêr’>

or

                                 êe_n><e_nçv> =  êe_n> <e_nêU> +  êe_n> d/dt <e_nêr’>

êe_n> d/dt <e_nêr’>, is the velocity of the particule relative to the origin O’ of  S’ expressed in the basis   íe_ný of  S. If we are interested in the relation between the coordinates of the velocity of the particule as measured by an observer in S and an observer in S’,  we introduce the unity operator êe_i><e_iç to obtain

                           êe_n><e_nçv> =  êe_n> <e_nêU> +  êe_n> d/dt <e_nêe_i><e_i êr’>

As the orientation of the basis  S’ and S are fixed then:  d/dt <e_nêe_i> = 0, and

                                 êe_n><e_nçv> = êe_n> <e_nêU> +   êe_n>  <e_nêe_i> d/dt <e_i êr’>     

 Where   d/dt <e_i êr’> = <e_i êv’> is the derivative of the components of r’ referred to the basis íçe_j>ý, then:

                                 êe_n><e_nçv> = êe_n> <e_nêU> +  êe_n>  <e_nêe_i>  <e_i êv’>   

This is the same as eq.(4) in the algebraic form.

Diferentiation of eq.(4) give similarly

                                          êa> = êA> +  êa’>

or in algebraic form

                    êe_n><e_nça> = êe_n> <e_nêA> +  êe_n>  <e_nêe_i> <e_i êa’>                                 

            êa> is the acceleration of the particule relative to O, and is the measured acceleration for an observer in S,  êA> is the acceleration of O’ relative to O, physicaly is the acceleration of the observer in S’ as observed by the observer in S; and   êa’> is the acceleration of the particule relative to O’, or the measured acceleration for an observer in S’.  

continue