$\angles{n\pars{t}}$: Dependencia Temporal
En secciones anteriores estudiamos el comportamiento de $\angles{n\pars{t}}$ $\pars{~n \equiv b\+b~}$ cuando la condición inicial se impone en $t_{0} \to -\infty$: El tiempo transcurrido desde el instante inicial $t_{0} \to -\infty$ hasta cualquier instante de tiempo finito $t$ tiende a $+\infty$ tal que el sistema alcanza una situación estacionaria ( independiente del tiempo ) lo cual es una conducta particular del sistema en estudio y, tal conducta, es derivada rigurosamente a partir del formalismo de Keldysh.
El hamiltoniano del sistema ( ver Gota Cuántica en Contacto con Varios Reservorios ) ( ver este enlace )
\begin{align} H_{0} & = \sum_{\eta\vec{k}}\epsilon_{\eta\vec{k}} a_{\eta\vec{k}}^{\dagger}a_{\eta\vec{k}}\ +\ \epsilon\,b^{\dagger}b\ +\ \sum_{\eta\vec{k}} \pars{V_{\eta\vec{k}}^{*}\,a_{\eta\vec{k}}^{\dagger}b\ +\ V_{\eta\vec{k}}\,b^{\dagger}a_{\eta\vec{k}}} \label{hamH089654} \\[5mm] H & = H_{0} - eV_{G} - e\sum_{\eta}V_{\eta} \nonumber \\ & = \sum_{\eta\vec{k}}\xi_{\eta\vec{k}}\, a_{\eta\vec{k}}^{\dagger}a_{\eta\vec{k}} + \xi\,b^{\dagger}b + {\cal V}\sum_{\eta\vec{k}} \pars{a_{\eta\vec{k}}^{\dagger}b + b^{\dagger}a_{\eta\vec{k}}} \label{HConPot1} \\ & \mbox{Por simplicidad:}\ V_{\eta\vec{k}} \equiv {\cal V} \in {\mathbb R}\nonumber \\[5mm]& \left\vert% \begin{array}{ccl} \xi_{\eta\vec{k}} & \equiv & \epsilon_{\eta\vec{k}} - eV_{\eta} \\[1mm] \xi & \equiv & \epsilon - eV_{G} \end{array}\right. \label{hamiltpot1} \end{align}- $t_{0} = 0$ es el instante inicial tal que el intervalo de tiempo transcurrido hasta un instante de tiempo finito $t$ es finito.
- Note que $A = A\pars{0}$ donde $A$ es un operador y $A\pars{t}$ es su representación de Heisenberg.
- $\rho\pars{0}$ es la matriz densidad en el instante inicial.
Ecuaciones de Heisenberg
$$ \ic\,\totald{b\pars{t}}{t} = \bracks{b\pars{t},H} = \xi b\pars{t} + {\cal V}\sum_{\eta\vec{k}}a_{\eta\vec{k}}\pars{t} $$ Evaluando la Transformada de Laplace en ambos miembros de esta ecuación se obtiene: \begin{equation} \pars{s + \xi\,\ic}b\pars{s}\ =\ \ob{b}{\ds{b\pars{t = 0}}}\ -\ \ic{\cal V}\sum_{\eta\vec{k}}a_{\eta\vec{k}}\pars{s} \label{dbdtvsaetak0} \end{equation}Similarmente, $$ \ic\,\totald{a_{\eta\vec{k}}\pars{t}}{t} = \bracks{a_{\eta\vec{k}}\pars{t},H} = \xi_{\eta\vec{k}}a_{\eta\vec{k}}\pars{t} + {\cal V}b\pars{t} $$ $$ \pars{s + \xi_{\eta\vec{k}}\,\ic}a_{\eta\vec{k}}\pars{s}\ =\ \ob{a_{\eta\vec{k}}}{\ds{a_{\eta\vec{k}}\pars{t = 0}}}\ -\ \ic{\cal V}b\pars{s} $$ \begin{equation} a_{\eta\vec{k}}\pars{s} = {a_{\eta\vec{k}} \over s + \xi_{\eta\vec{k}}\ic} - \ic{\cal V}\,{b\pars{s} \over s + \xi_{\eta\vec{k}}\ic} \label{aetakvsbt0} \end{equation} Reemplazando la expresión \eqref{aetakvsbt0} en la Ec. \eqref{dbdtvsaetak0}: \begin{align*} \pars{s + \xi\,\ic}b\pars{s} & = b -\ic{\cal V}\sum_{\eta\vec{k}} {a_{\eta\vec{k}} \over s + \xi_{\eta\vec{k}}\,\ic} - \pars{{\cal V}^{2}\sum_{\eta\vec{k}} {1 \over s + \xi_{\eta\vec{k}}\,\ic}}b\pars{s} \end{align*} \begin{align} b\pars{s} & = {b \over s + \xi\,\ic + {\cal V}^{2}\sum_{\eta'\vec{k}'} {1 \over s + \xi_{\eta'\vec{k}'}\,\ic}} \nonumber \\[3mm] & \mbox{} -\ic\,{{\cal V} \over s + \xi\,\ic + {\cal V}^{2}\sum_{\eta'\vec{k}'} {1 \over s + \xi_{\eta'\vec{k}'}\,\ic}} \sum_{\eta\vec{k}}{a_{\eta\vec{k}} \over s + \xi_{\eta\vec{k}}\,\ic} \label{bsexacta0BB} \end{align} En la Aproximación de Banda Ancha ( ver Solo un Conductor ( El Límite de Banda Ancha ) ), la suma en los denominadores se reduce a: \begin{align} \sum_{\eta'\vec{k}'}{1 \over s + \xi_{\eta'\vec{k}'}\,\ic} & = \sum_{\eta'}\dos_{\eta'}\pars{0} \int_{-\infty}^{\infty}{\dd\xi \over s + \xi\,\ic} = \sum_{\eta'}\dos_{\eta'}\pars{0} \int_{-\infty}^{\infty}{s \over \xi^{2} + s^{2}}\,\dd\xi \nonumber \\[3mm] = \pi\sum_{\eta'}\dos_{\eta'}\pars{0} \label{approxBA89765} \end{align} El resultado \eqref{bsexacta0BB} se reduce a \begin{align} b\pars{s} & = {b \over s + \xi\,\ic + \Gamma} -\ic\,{{\cal V} \over s + \xi\,\ic + \Gamma} \sum_{\eta\vec{k}}{a_{\eta\vec{k}} \over s + \xi_{\eta\vec{k}}\,\ic} \\ & \mbox{con}\ \Gamma \equiv \sum_{\eta}\Gamma_{\eta}\,,\quad \Gamma_{\eta} \equiv \pi{\cal V}^{2}\dos_{\eta}\pars{0} \end{align} \begin{align} b\pars{t} & = \int_{0^{+} - \infty\ic}^{0^{+} + \infty\ic} b\pars{s}\expo{st}\,{\dd s \over 2\pi\ic} = b\int_{0^{+} - \infty\ic}^{0^{+} + \infty\ic} {\expo{st} \over s + \xi\,\ic + \Gamma}\,{\dd s \over 2\pi\ic} \nonumber \\[3mm] & \mbox{} -\ic{\cal V}\sum_{\eta\vec{k}} {a_{\eta\vec{k}} \over \pars{\xi - \xi_{\eta\vec{k}}}\ic + \Gamma} \times \nonumber \\[3mm] & \mbox{} \bracks{% \int_{0^{+} - \infty\ic}^{0^{+} + \infty\ic} {\expo{st} \over s + \xi_{\eta\vec{k}}\,\ic}\,{\dd s \over 2\pi\ic} - \int_{0^{+} - \infty\ic}^{0^{+} + \infty\ic} {\expo{st} \over s + \xi\,\ic + \Gamma}\,{\dd s \over 2\pi\ic}}\,, \quad t > 0 \end{align} \begin{equation} \left\lbrace\begin{array}{rcl} b\pars{t} & = & b\expo{-\ic\xi t}\expo{-\Gamma t} + {\cal V}\sum_{\eta\vec{k}} {a_{\eta\vec{k}} \over \xi_{\eta\vec{k}} - \xi + \Gamma\,\ic} \pars{\expo{-\ic\xi_{\eta\vec{k}}t} - \expo{-\ic\xi t}\expo{-\Gamma t}} \\[1mm] b\+\pars{t} & = & b\+\expo{\ic\xi t}\expo{-\Gamma t} + {\cal V}\sum_{\eta\vec{k}} {a_{\eta\vec{k}}\+ \over \xi_{\eta\vec{k}} - \xi - \Gamma\,\ic} \pars{\expo{\ic\xi_{\eta\vec{k}}t} - \expo{\ic\xi t}\expo{-\Gamma t}} \end{array}\right. \end{equation}
$\ds{1 \over \Gamma}$ $\ds{\pars{~\mbox{0/y}\
{\hbar \over \Gamma}~}}$ es una escala de tiempo que
determina la
rapidezcon que el sistema
se encuentra en las inmediacionesdel estado estacionario.
Con $n\pars{t} = b\+\pars{t}b\pars{t}$ y $n = b\+b = n\pars{0}$: \begin{align*} n\pars{t} & = n\expo{-2\Gamma t} + {\cal V}^{2}\sum_{\eta\vec{k} \atop \eta'\vec{k}'} {\pars{\expo{\ic\xi_{\eta\vec{k}}t} - \expo{\ic\xi t}\expo{-\Gamma t}} \pars{\expo{-\ic\xi_{\eta'\vec{k}'}t} - \expo{-\ic\xi t}\expo{-\Gamma t}} \over \pars{\xi_{\eta\vec{k}} - \xi - \Gamma\,\ic} \pars{\xi_{\eta'\vec{k}'} - \xi + \Gamma\,\ic}}\, a_{\eta\vec{k}}\+a_{\eta'\vec{k}'} \\[3mm] & \mbox{} + \bracks{% \expo{\ic\xi t}\expo{-\Gamma t} {\cal V}\sum_{\eta\vec{k}} {b\+a_{\eta\vec{k}} \over \xi_{\eta\vec{k}} - \xi + \Gamma\,\ic} \pars{\expo{-\ic\xi_{\eta\vec{k}}t} - \expo{-\ic\xi t}\expo{-\Gamma t}} + {\rm H.C.}} \end{align*}
Multiplicando ambos miembros de la última expresión por $\rho\pars{0}$ ( la matriz densidad en el instante incial $t_{0} = 0$ ) y evaluando la traza sobre los estados del sistema $\pars{~\vphantom{\LARGE A}\angles{\cdots} = \trace\pars{\rho\pars{0}\ldots}~}$: \begin{align} \angles{n\pars{t}} & = \angles{n\pars{0}}\expo{-2\Gamma t} \nonumber \\[3mm] & \mbox{} + {\cal V}^{2}\sum_{\eta\vec{k} \atop \eta'\vec{k}'} {\pars{\expo{\ic\xi_{\eta\vec{k}}t} - \expo{\ic\xi t}\expo{-\Gamma t}} \pars{\expo{-\ic\xi_{\eta'\vec{k}'}t} - \expo{-\ic\xi t}\expo{-\Gamma t}} \over \pars{\xi_{\eta\vec{k}} - \xi - \Gamma\,\ic} \pars{\xi_{\eta'\vec{k}'} - \xi + \Gamma\,\ic}}\, \angles{a_{\eta\vec{k}}\+\pars{0}a_{\eta'\vec{k}'}\pars{0}} \nonumber \\[3mm] & \mbox{} + 2\,\Re\pars{% \expo{\ic\xi t}\expo{-\Gamma t} {\cal V}\sum_{\eta\vec{k}} {\angles{b\+\pars{0}a_{\eta\vec{k}}\pars{0}} \over \xi_{\eta\vec{k}} - \xi + \Gamma\,\ic} \pars{\expo{-\ic\xi_{\eta\vec{k}}t} - \expo{-\ic\xi t}\expo{-\Gamma t}}} \label{nvstexacta0001} \end{align}
Un caso particularmente interesante ocurre cuando los
reservorios se encuentran en equilibrio termodinámico en el
instante inicial $t_{0} = 0$:
$$
\rho\pars{0} \propto \expo{-\beta\pars{H_{0} - \mu N}}\,,\qquad
\pars{~\mbox{ver}\ \eqref{hamH089654}~}
$$
$\rho\pars{0}$ es la matriz densidad en el instante inicial
$t_{0} = 0$. $\ds{\beta = {1 \over \kb T}}$. $T$ es la
temperatura y $\mu$ es el potencial químico.
$\mu \gg \kb T$.
$$
\angles{a_{\eta\vec{k}}\+\pars{0}a_{\eta'\vec{k}'}\pars{0}}
= \delta_{\eta\eta'}\delta_{\vec{k}\vec{k}'}
\fermi\pars{\epsilon_{\eta\vec{k}} - \mu}
\,,\qquad
\angles{b\+\pars{0}a_{\eta\vec{k}}\pars{0}} = 0
$$
$\fermi\pars{\omega} \equiv \pars{\expo{\beta\omega} + 1}^{-1}$
es la función de distribución de Fermi-Dirac.
En tal caso, $\angles{n\pars{t}}$ se reduce a $\pars{~\mbox{ver}\
\eqref{nvstexacta0001}~}$:
\begin{align*}
\angles{n\pars{t}} & =
\angles{n\pars{0}}\expo{-2\Gamma t} +
{\cal V}^{2}\sum_{\eta\vec{k}}
{\verts{\expo{\ic\pars{\xi_{\eta\vec{k}} - \xi}t} -
\expo{-\Gamma t}}^{2}
\over
\pars{\xi_{\eta\vec{k}} - \xi}^{2} + \Gamma^{2}}\,
\fermi\pars{\xi_{\eta\vec{k}} + eV_{\eta} - \mu}
\\[5mm] & =
\angles{n\pars{0}}\expo{-2\Gamma t}
\\[3mm] & \mbox{} +
{\cal V}^{2}\sum_{\eta\vec{k}}
{1 - 2\cos\pars{\bracks{\xi_{\eta\vec{k}} - \xi}t}\expo{-\Gamma t}
+ \expo{-2\Gamma t}
\over
\pars{\xi_{\eta\vec{k}} - \xi}^{2} + \Gamma^{2}}\,
\fermi\pars{\xi_{\eta\vec{k}} + eV_{\eta} - \mu}
\end{align*}
\begin{align*}
\angles{n\pars{t}} & =
\angles{n\pars{0}}\expo{-2\Gamma t}
\\[3mm] & \mbox{} -
2\expo{-\Gamma t}\,\sum_{\eta}{\Gamma_{\eta} \over \Gamma}
\int_{-\infty}^{\infty}
{\Gamma/\pi
\over
\pars{\omega - \wt{\xi}_{\eta}}^{2} + \Gamma^{2}}\,
\cos\pars{\bracks{\omega - \wt{\xi}_{\eta}}t}\fermi\pars{\omega}\,
\dd\omega
\\[3mm] & \mbox{} +
\pars{1 + \expo{-2\Gamma t}}\angles{n\pars{\infty}}
\end{align*}
donde
$\wt{\xi}_{\eta} \equiv \xi - \mu + eV_{\eta} =
\epsilon - \mu - e\pars{V_{G} - V_{\eta}}$ y
\begin{align*}
\angles{n\pars{\infty}} & =
\sum_{\eta}{\Gamma_{\eta} \over \Gamma}
\int_{-\infty}^{\infty}
{\Gamma/\pi \over \pars{\omega - \wt{\xi}_{\eta}}^{2} + \Gamma^{2}}
\,\fermi\pars{\omega}\,\dd\omega
\\[3mm] & = \half - \sum_{\eta}{\Gamma_{\eta} \over \Gamma}
\bracks{{1 \over \pi}\,\Im
\Psi\pars{\half + {\Gamma + \wt{\xi}_{\eta}\,\ic \over 2\pi\kb T}}}
\end{align*}
$\Psi\pars{z}$ es la función Digamma
( ver
Apéndice
Utilidades ). Cuando $\ds{t \gg {1 \over \Gamma}}$
$\ds{\pars{~\mbox{o/y}\ t \gg {\hbar \over \Gamma}~}}$ se cumple que
$\ds{\angles{n\pars{t}} \approx \angles{n\pars{\infty}}}$.
electrón solitario. Ver la sección Dos Conductores.
En tal caso, $\angles{n\pars{t}}$ viene dado por ( ver expresión \eqref{nvstexacta0001} ):
\begin{align*} \angles{n\pars{t}} & = \angles{n\pars{0}}\expo{-2\Gamma t} + {\cal V}^{2} {1 - 2\cos\pars{\bracks{\epsilon_{R\vec{p}} - E}t}\expo{-\Gamma t} + \expo{-2\Gamma t} \over \pars{\epsilon_{R\vec{p}} - E}^{2} + \Gamma^{2}} \\[3mm] & = \angles{n\pars{0}}\expo{-2\Gamma t} \\[3mm] & \mbox{} + \delta {\Gamma/\pi \over \pars{\epsilon_{R\vec{p}} - E}^{2} + \Gamma^{2}}\, \braces{\vphantom{\LARGE A}% 1 - 2\cos\pars{\bracks{\epsilon_{R\vec{p}} - E}t} \expo{-\Gamma t} + \expo{-2\Gamma t}} \end{align*} donde $E = \epsilon - e\pars{V_{G} - V_{R}}$ y $\delta \equiv 1/\sum_{\eta}\dos_{\eta}\pars{0}$. Note que, por simplicidad, continuamos usando la aproximación \eqref{approxBA89765}.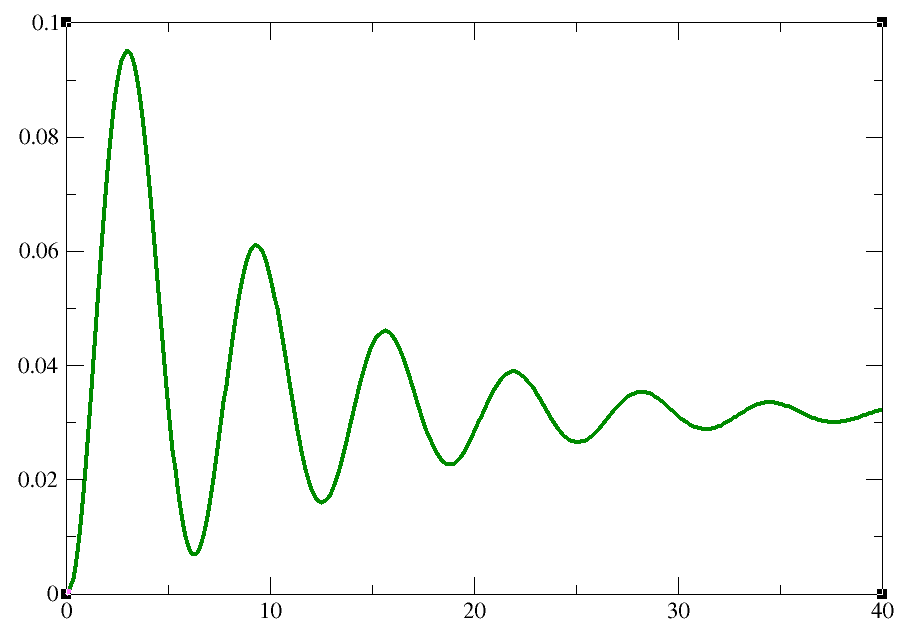
${\large t}$
La
datade la figura es generada por el programa, en
C++, gotaC_0.cc ( ver
Apéndice
Utilidades ). Cuando $\omega = 0$
( resonancia) las oscilaciones desaparecen y se observa un decaimiento hacía la solución estacionaria.
Ecuaciones de Kadanoff-Baym
En esta sección estudiaremos las ecuaciones de Kadanoff-Baym ( ver Bibliografía ) con el propósito de estudiar una ecuación de movimiento para $\angles{n\pars{t}}$. Para ello es conveniente usar la Conservación del Número de Partículas $\ds{\dd\angles{n\pars{t}}/\dd t = -\,\pars{1/e}\,\sum_{\eta}\angles{{\cal I}_{\eta}\pars{t}}}$. Ver expresión para $\angles{{\cal I}_{\eta}\pars{t}}$.
\begin{align} \totald{\angles{n\pars{t}}}{t} & = -\,{2 \over \hbar}\,\Re\int_{0}^{\infty} \bracks{\Sigma^{\rm\pars{r}}\pars{t - t'}{\rm G}^{<}\pars{t',t} + \Sigma^{<}\pars{t - t'}{\rm G}^{\rm\pars{a}}\pars{t',t}}\,\dd t' \label{IvsGttprima000} \\[3mm] \mbox{donde} & \Sigma^{{\rm \pars{r}} \atop <}\pars{t} = \sum_{\eta}\Sigma_{\eta}^{{\rm \pars{r}} \atop <}\pars{t} = {\cal V}^{2}\sum_{\eta}\sum_{\vec{k}} {\rm g}_{\eta\vec{k}}^{{\rm \pars{r}} \atop <}\pars{t} \end{align} $t_{0} = 0$ es el instante inicial y, por simplicidad, $V_{\eta\vec{k}} \equiv {\cal V} \in {\mathbb R}$. Note que $\angles{n\pars{t}} = -\ic{\rm G}^{<}\pars{t,t}$.La transformada de Fourier de $\Sigma_{\eta}^{\rm\pars{r}}\pars{t}$ viene dada por $ {\cal V}^{2}\sum_{\vec{k}} \pars{\omega - \xi_{\eta\vec{k}} + \ic 0^{+}}^{-1}$ la cual se reduce en el límite de banda ancha a
\begin{equation} -\ic\pi{\cal V}^{2}\dos_{\eta}\pars{0} = -\ic\Gamma_{\eta} \quad\mbox{tal que}\quad \Sigma^{\rm\pars{r}}\pars{t} = -\ic\Gamma\delta\pars{t} \label{lbaSr451789} \end{equation} Este resultado conduce, con la Ec. \eqref{IvsGttprima000}, a \begin{equation} \totald{\angles{n\pars{t}}}{t} + 2\Gamma\angles{n\pars{t}} = -2\,\Re\int_{0}^{\infty} \Sigma^{<}\pars{t - t'}{\rm G}^{\rm\pars{a}}\pars{t',t}\,\dd t'\,, \quad\hbar = 1 \label{nvstparcial96728876} \end{equation} ${\rm G^{\rm\pars{a}}}\pars{t,t'}$ satisface la ecuación diferencial $$ \pars{\ic\,\partiald{}{t} - \xi}{\rm G^{\rm\pars{a}}}\pars{t,t'} = \delta\pars{t - t'} + \int_{0}^{\infty}\Sigma^{\pars{a}}\pars{t - t''} {\rm G^{\pars{a}}}\pars{t'',t'}\,\dd t'' $$ puesto que ${\rm g^{\rm\pars{a}}}\pars{t} = \ic\Theta\pars{-t}\expo{-\ic\xi t}$ satisface $\pars{\ic\,\partial_{t} - \xi}{\rm g^{\rm\pars{a}}}\pars{t} = \delta\pars{t}$. Similarmente $\pars{~\mbox{ver} \eqref{lbaSr451789}~}$, $\Sigma^{\rm\pars{a}}\pars{t} = \ic\Gamma\delta\pars{t}$ en el límite de banda ancha. ${\rm G^{\rm\pars{a}}}\pars{t,t'}$ satisface la ecuación diferencial $$ \pars{\ic\,\partiald{}{t} - \xi - \Gamma\,\ic} {\rm G^{\rm\pars{a}}}\pars{t,t'} = \delta\pars{t - t'} $$ $$ \imp\quad {\rm G^{\rm\pars{a}}}\pars{t,t'} = \ic\Theta\pars{t' - t}\expo{-\ic\pars{\xi + \Gamma\,\ic}\pars{t - t'}} $$ La Ec. \eqref{nvstparcial96728876} se reduce a la Ecuación de Langevin \begin{align} \totald{\angles{n\pars{t}}}{t} + 2\Gamma\angles{n\pars{t}} & = {\cal F}\pars{t} \label{nvstlangevin} \\ \mbox{donde}\ {\cal F}\pars{t} & \equiv 2\,\Im\int_{0}^{t} \Sigma^{<}\pars{t'}\expo{\ic\pars{\xi + \Gamma\,\ic}t'}\,\dd t' \label{flangevin} \end{align} Ec. \eqref{nvstlangevin} muestra que $\angles{n\pars{t}}$ tiende a decaer bajo la acción de los contactos con los reservorios pero a su vez es afectada por la influencia de ${\cal F}\pars{t}$. ${\cal F}\pars{t}$ es similar a una fuerza al azar (Random Force
El lector puede usar los resultados \eqref{nvstfuncF879990} y
\eqref{Fvst564990} para revisar, por ejemplo, algunos casos
límites o/y estudiar numéricamente una
solución general.