Ecuaciones de Kadanoff-Baym. Ejemplo: Bosones
El objeto de la presente nota es estudiar la variación de
energía
$$
{\cal P}\pars{t} \equiv
\totald{\angles{\varepsilon\,a\+\pars{t}a\pars{t}}}{t}
$$
del oscilador armónico bajo la acción de un reservorio
de bosones.
Con este ejemplo queremos mostrar el uso de las ecuaciones de Kadanoff-Baym las cuales se derivan directamente sin recurrir al formalismo de Keldysh.
Con este ejemplo queremos mostrar el uso de las ecuaciones de Kadanoff-Baym las cuales se derivan directamente sin recurrir al formalismo de Keldysh.
El hamiltoniano del sistema viene dado por
\begin{equation} H\ =\ \ob{\varepsilon a\+a}{\mbox{Oscilador Armónico}}\ +\ \ob{\sum_{\vec{k}}\omega_{\vec{k}}b_{\vec{k}}\+ b_{\vec{k}}} {\mbox{Bosones Libres}}\ +\ \ob{{\cal V}\sum_{\vec{k}}\pars{a\+ b_{\vec{k}} + b_{\vec{k}}\+ a}} {\mbox{Interacción}} \end{equation} donde $\varepsilon > 0,\ \omega_{\vec{k}} > 0$ y $$ \bracks{a,a\+} = 1\,,\quad \bracks{b_{\vec{k}},b_{\vec{q}}} = 0\,,\quad \bracks{b_{\vec{k}},b_{\vec{q}}\+} = \delta_{\vec{k}\vec{q}}\,,\quad \bracks{a,b_{\vec{k}}} = 0\,,\quad \bracks{a,b_{\vec{k}}\+} = 0 $$ ${\cal V}$ es la constante de acoplamiento. \begin{align*} {\cal P}\pars{t} & = \varepsilon\,\totald{\angles{a\+\pars{t}a\pars{t}}}{t} = \varepsilon\braces{-\,{\ic \over \hbar}\, \angles{\bracks{a\+\pars{t}a\pars{t},H\pars{t}}}} \\[3mm] & = -\ic\,{\varepsilon \over \hbar}\, \angles{\bracks{a\+\pars{t}a\pars{t},{\cal V}\sum_{\vec{k}}\braces{% a\+\pars{t}b_{\vec{k}}\pars{t} + b_{\vec{k}}\+\pars{t}a\pars{t}}}} \\[3mm] & = -\ic\,{\varepsilon \over \hbar}\sum_{\vec{k}} \angles{{\cal V}\bracks{% a\+\pars{t}b_{\vec{k}}\pars{t} - b_{\vec{k}}\+\pars{t}a\pars{t}}} \\[3mm] & = -\ic\,{\varepsilon \over \hbar}\,{\cal V}\sum_{\vec{k}}\bracks{% \angles{a\+\pars{t}b_{\vec{k}}\pars{t}} - \angles{b_{\vec{k}}\+\pars{t}a\pars{t}}} \end{align*}
\begin{equation}
{\cal P}\pars{t} =
{2\varepsilon \over \hbar}\,{\cal V}\,\Im\sum_{\vec{k}}
\angles{a\+\pars{t}b_{\vec{k}}\pars{t}}
\label{defP0BB}
\end{equation}
Introduzcamos la función de Green ( Kadanoff-Baym )
\begin{equation} {\rm F}_{\vec{k}}\pars{t,t'} \equiv -\ic\angles{a\+\pars{t}b_{\vec{k}}\pars{t'}} \label{defFkBB} \end{equation} la cual corresponde a una función de Green-Keldysh mayor.
\begin{equation}
{\cal P}\pars{t} =
{2\varepsilon \over \hbar}\,{\cal V}\,\Re\sum_{\vec{k}}
{\rm F}_{\vec{k}}\pars{t,t}
\label{defP1BB}
\end{equation}
${\rm F}_{\vec{k}}\pars{t,t'}$ $\pars{~\mbox{ver
definición}\ \eqref{defFkBB}~}$ satisface la ecuación de
movimiento
\begin{align*}
\ic\,\partiald{{\rm F}_{\vec{k}}\pars{t,t'}}{t} & =
\angles{\totald{a\+\pars{t}}{t}\,b_{\vec{k}}\pars{t'}}
=
\angles{-\ic\bracks{a\+\pars{t},H}b_{\vec{k}}\pars{t'}}
\\ & = -\ic\angles{\bracks{-\varepsilon a\+\pars{t} -
{\cal V}\sum_{\vec{q}}b_{\vec{q}}\+\pars{t}}b_{\vec{k}}\pars{t'}}\,,
\qquad\hbar = 1
\end{align*}
\begin{equation}
\pars{\ic\,\partiald{}{t} + \varepsilon}{\rm F}_{\vec{k}}\pars{t,t'} =
-{\cal V}\sum_{\vec{q}}{\rm G}_{\vec{q}\vec{k}}\pars{t,t'}
\label{FvsGBB}
\end{equation}
\begin{equation}
\mbox{donde}\quad{\rm G}_{\vec{q}\vec{k}}\pars{t,t'} \equiv
-\ic\angles{b_{\vec{q}}\+\pars{t}b_{\vec{k}}\pars{t'}}
\label{defGqk100BB}
\end{equation}
la cual satisface
\begin{align*}
\ic\partiald{{\rm G}_{\vec{q}\vec{k}}\pars{t,t'}}{t} & =
\angles{\totald{b_{\vec{q}}\+\pars{t}}{t}\,b_{\vec{k}}\pars{t'}} =
\angles{-\ic\bracks{b_{\vec{q}}\+\pars{t},H}b_{\vec{k}}\pars{t'}}
\\ & =
-\ic \angles{\bracks{-\omega_{\vec{q}}b_{\vec{q}}\+\pars{t} -
{\cal V}a\+\pars{t}}b_{\vec{k}}\pars{t'}}
\end{align*}
\begin{equation}
\pars{\ic\,\partiald{}{t} + \omega_{\vec{q}}}
{\rm G}_{\vec{q}\vec{k}}\pars{t,t'} =
- {\cal V}{\rm F}_{\vec{k}}\pars{t,t'}
\label{GvsFBB}
\end{equation}
\eqref{FvsGBB} y \eqref{GvsFBB} son ecuaciones acopladas para
${\rm F}_{\vec{k}}\pars{t,t'}$ y ${\rm G}_{\vec{q}\vec{k}}\pars{t,t'}$:
\begin{align}
\pars{\ic\,\partiald{}{t} + \varepsilon}{\rm F}_{\vec{k}}\pars{t,t'} & =
-{\cal V}\sum_{\vec{q}}{\rm G}_{\vec{q}\vec{k}}\pars{t,t'}
\label{acoplada0BB}
\\
\pars{\ic\,\partiald{}{t} + \omega_{\vec{q}}}
{\rm G}_{\vec{q}\vec{k}}\pars{t,t'} & =
- {\cal V}{\rm F}_{\vec{k}}\pars{t,t'}
\label{acoplada1BB}
\end{align}
Ecs. \eqref{acoplada0BB} y \eqref{acoplada1BB} pueden ser reescritas en
la forma:
\begin{align}
\pars{\ic\,\partiald{}{t} + \varepsilon}
\bracks{{\rm F}_{\vec{k}}\pars{t,t'} -
{\rm f}_{\vec{k}}\pars{t,t'}} & =
- {\cal V}\sum_{\vec{q}}{\rm G}_{\vec{q}\vec{k}}\pars{t,t'}
\label{acoplaGgF100BB}
\\[3mm]
\pars{\ic\,\partiald{}{t} + \omega_{\vec{q}}}
\bracks{{\rm G}_{\vec{q}\vec{k}}\pars{t,t'} -
{\rm g}_{\vec{q}\vec{k}}\pars{t,t'}} & =
- {\cal V}{\rm F}_{\vec{k}}\pars{t,t'}
\label{acoplaGgF1000BB}
\end{align}
donde
$\pars{~\mbox{ver definiciones}\ \eqref{defFkBB}\ \mbox{y}\
\eqref{defGqk100BB}~}$
\begin{align}
{\rm f}_{\vec{k}}\pars{t,t'} & =
{\rm F}_{\vec{k}}\pars{t,t'}_{{\cal V}\ =\ 0} =
-\ic\angles{a\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}_{{\cal V}\ =\ 0}
\expo{\ic\bracks{\varepsilon\pars{t - t_{0}} -
\omega_{\vec{k}}\pars{t' - t_{0}}}}
\label{deffkttp85467BB}
\\[3mm]
{\rm g}_{\vec{q}\vec{k}}\pars{t,t'} & =
{\rm G}_{\vec{q}\vec{k}}\pars{t,t'}_{{\cal V}\ =\ 0} =
-\ic\angles{b_{\vec{q}}\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}
_{{\cal V}\ =\ 0}
\expo{\ic\bracks{\omega_{\vec{q}}\pars{t - t_{0}} -
\omega_{\vec{k}}\pars{t' - t_{0}}}}
\label{defgqkttp76844BB}
\end{align}
$t_{0}$ es el Instante Inicial.
Note que
$\angles{a\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}_{{\cal V}\ =\ 0}$ y
$\angles{b_{\vec{q}}\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}$ son valores
medios en el instante inicial $t_{0}$ $\pars{~\mbox{cuando}\
{\cal V = 0~}}$.
$\angles{\cdots} \equiv \trace\pars{\rho\pars{t_{0}}\ldots}$ donde
$\rho\pars{t_{0}}$ es la matriz densidad en el instante inicial
$t_{0}$.
Ecs. \eqref{acoplaGgF100BB} y \eqref{acoplaGgF1000BB} son reescritas en la forma integral
\begin{align} {\rm F}_{\vec{k}}\pars{t,t'} & = {\rm f}_{\vec{k}}\pars{t,t'} + \int_{-\infty}^{\infty}{\rm g}\pars{t - t''}\bracks{% -{\cal V}\sum_{\vec{q}}{\rm G}_{\vec{q}\vec{k}}\pars{t'',t'}}\,\dd t'' \label{GvsFint3006BB} \\[3mm] {\rm G}_{\vec{q}\vec{k}}\pars{t,t'} & = {\rm g}_{\vec{q}\vec{k}}\pars{t,t'} + \int_{-\infty}^{\infty}{\rm g}_{\vec{q}}\pars{t - t''}\bracks{% -{\cal V}{\rm F}_{\vec{k}}\pars{t'',t'}}\,\dd t'' \label{GvsFint3876BB} \end{align} donde \begin{align} {\rm g}\pars{t} & \equiv \ic\Theta\pars{-t}\expo{\ic\varepsilon t}\,,\quad \pars{\ic\,\partiald{}{t} + \varepsilon}{\rm g}\pars{t} = \delta\pars{t} \label{defgttp4678990BB} \\[3mm] {\rm g}_{\vec{q}}\pars{t} & = \ic\Theta\pars{-t}\expo{\ic\omega_{\vec{q}}t}\,,\quad \pars{\ic\,\partiald{}{t} + \omega_{\vec{q}}} {\rm g}_{\vec{q}}\pars{t} = \delta\pars{t} \label{defgqttp3338990BB} \end{align}
Note que
$\varphi\pars{t} \equiv
\ic\Theta\pars{-t}\expo{\ic Et}$ satisface
$$
\ic\,\partiald{\varphi\pars{t}}{t} =
\delta\pars{t} - \Theta\pars{-t}\expo{\ic Et}\pars{\ic E}
$$
$$
\mbox{tal que}\
\pars{\ic\,\partiald{}{t} + E}\varphi\pars{t} = \delta\pars{t}
$$
.
Con la substitución de la expresión \eqref{GvsFint3876BB}
en la Ec. \eqref{GvsFint3006BB}, esta se reduce a
\begin{align}
{\rm F}_{\vec{k}}\pars{t,t'} & = {\rm f}_{\vec{k}}\pars{t,t'}
\nonumber
\\[3mm] & - {\cal V}\int_{-\infty}^{\infty}{\rm g}\pars{t - t''}
\sum_{\vec{q}}\bracks{%
{\rm g}_{\vec{q}\vec{k}}\pars{t'',t'}
-{\cal V} \int_{-\infty}^{\infty}{\rm g}_{\vec{q}}\pars{t'' - t'''}
{\rm F}_{\vec{k}}\pars{t''',t'}\,\dd t'''}\,\dd t''
\nonumber
\\[5mm] & = {\rm f}_{\vec{k}}\pars{t,t'}
- {\cal V}\int_{-\infty}^{\infty}{\rm g}\pars{t - t''}
\sum_{\vec{q}}{\rm g}_{\vec{q}\vec{k}}\pars{t'',t'}\,\dd t''
\nonumber
\\[3mm] & + \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}
{\rm g}\pars{\bracks{t - t'''} - t''}\bracks{{\cal V}^{2}\sum_{\vec{q}}
{\rm g}_{\vec{q}}\pars{t''}}{\rm F}_{\vec{k}}\pars{t''',t'}\,
\dd t'''\,\dd t''
\end{align}
\begin{align}
{\rm F}_{\vec{k}}\pars{t,t'} & = {\rm f}_{\vec{k}}\pars{t,t'}
- {\cal V}\int_{-\infty}^{\infty}{\rm g}\pars{t - t''}
\sum_{\vec{q}}{\rm g}_{\vec{q}\vec{k}}\pars{t'',t'}\,\dd t''
\nonumber
\\[3mm] & + \int_{-\infty}^{\infty}
{\rm K}\pars{t - t''}{\rm F}_{\vec{k}}\pars{t'',t'}\,\dd t''
\label{ecintFkttp9876BB}
\\[5mm]
{\rm K}\pars{t} & \equiv
\int_{-\infty}^{\infty}
{\rm g}\pars{t - t'}\Sigma\pars{t'}
\,\dd t'
\label{defKttpBB}
\\[3mm]
\Sigma\pars{t} & \equiv
{\cal V}^{2}\sum_{\vec{q}}{\rm g}_{\vec{q}}\pars{t}
\label{defSigmat89999BB}
\end{align}
La Transformada de Fourier de ${\rm K}\pars{t - t'}$
$\pars{~\mbox{definición}\ \eqref{defKttpBB}~}$
viene dada por
( ver Apéndice
Utilidades )
$$
{\rm K}\pars{\omega,\omega'} =
2\pi\delta\pars{\omega - \omega'}{\rm g}\pars{\omega}\Sigma\pars{\omega}
$$
tal que $\pars{~\mbox{ver Ec.}\ \eqref{ecintFkttp9876BB}~}$
$$
{\rm F}_{\vec{k}}\pars{\omega,\omega'} =
\fermi_{\vec{k}}\pars{\omega,\omega'} - {\cal V}{\rm g}\pars{\omega}
\sum_{\vec{q}}{\rm g}_{\vec{q}\vec{k}}\pars{\omega,\omega'}
+
{\rm g}\pars{\omega}\Sigma\pars{\omega}
{\rm F}_{\vec{k}}\pars{\omega,\omega'}
$$
\begin{equation}
{\rm F}_{\vec{k}}\pars{\omega,\omega'} =
{\fermi_{\vec{k}}\pars{\omega,\omega'}/{\rm g}\pars{\omega} -
{\cal V}\sum_{\vec{q}}{\rm g}_{\vec{q}\vec{k}}\pars{\omega,\omega'}
\over 1/{\rm g}\pars{\omega} - \Sigma\pars{\omega}}
\label{solgenFkoopBB}
\end{equation}
\begin{equation}
{\cal P}\pars{t} =
{2\varepsilon \over \hbar}\,{\cal V}\,\Re\sum_{\vec{k}}
\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}
{\rm F}_{\vec{k}}\pars{\omega,\omega'}\expo{-\ic\pars{\omega - \omega'}t}
\,{\dd\omega\,\dd\omega' \over \pars{2\pi}^{2}}\,,\quad
\pars{~\mbox{ver}\ \eqref{defP1BB}~}
\label{defP0653456BB}
\end{equation}
Note que
( ver Apéndice
Utilidades )
- $\ds{{\rm f}_{\vec{k}}\pars{\omega,\omega'} = -\pars{2\pi}^{2}\ic \angles{a\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}_{{\cal V}\ =\ 0} \expo{\ic\pars{\omega_{\vec{k}} - \varepsilon}t_{0}} \delta\pars{\omega + \varepsilon} \delta\pars{\omega' + \omega_{\vec{k}}}}$. Ver expresión \eqref{deffkttp85467BB}.
- $\ds{{\rm g}\pars{\omega} = {1 \over \omega + \varepsilon - \ic 0^{+}}}$. Ver definición \eqref{defgttp4678990BB}.
- $\ds{{\rm g}_{\vec{q}\vec{k}}\pars{\omega,\omega'} = -\pars{2\pi}^{2}\ic \angles{b_{\vec{q}}\+\pars{t_{0}} b_{\vec{k}}\pars{t_{0}}}_{{\cal V}\ =\ 0} \expo{\ic\pars{\omega_{\vec{k}} - \omega_{\vec{q}}}t_{0}} \delta\pars{\omega + \omega_{\vec{q}}} \delta\pars{\omega' + \omega_{\vec{k}}}}$. Ver expresión \eqref{defgqkttp76844BB}.
- $\ds{{\rm g}_{\vec{q}}\pars{\omega} = {1 \over \omega + \omega_{\vec{q}} - \ic 0^{+}}}$. Ver definición \eqref{defgqttp3338990BB}.
- y $\pars{~\mbox{ver definición}\ \eqref{defSigmat89999BB}~}$
$$
\Sigma\pars{\omega} =
{\cal V}^{2}\sum_{\vec{q}}{\rm g}_{\vec{q}}\pars{\omega} =
{\cal V}^{2}
\pp\sum_{\vec{q}}{1 \over \omega + \omega_{\vec{q}}} +
\ic\pi{\cal V}^{2}\dos_{\rm B}\pars{-\omega}
$$
$\ds{\dos_{\rm B}\pars{\omega} \equiv
\sum_{\vec{q}}\delta\pars{\omega - \omega_{\vec{q}}}}$ es la
Densidad de Estados de los Bosones en el Reservorio.
Por simplicidad, despreciamos la parte principal tal que
$$ \Sigma\pars{\omega} = \ic\pi{\cal V}^{2}\dos_{\rm B}\pars{-\omega} $$
Exploraremos los modelos siguientes de $\dos_{\rm B}\pars{\omega}$ en
la elaboración de ejemplos particulares. $\Omega$ es el
Volumen del Sistema.
- $\large\ds{\omega_{\vec{k}} \equiv sk\,,\ s > 0}$. Esta elección describe, por ejemplo, un modelo simple de un gas de fonones donde $s$ es la Velocidad del Sonido o un gas de fotones donde $s = c$ es la Velocidad de la Luz, etc$\ldots$. $$ \dos_{\rm s}\pars{\omega} = \sum_{\vec{k}}\delta\pars{\omega - sk} = {\Omega \over \pars{2\pi}^{3}}\int_{0}^{\infty} {\delta\pars{k - \omega/s} \over s}\,4\pi k^{2}\,\dd k $$ \begin{equation} \begin{array}{|c|} \hline\\ \mbox{}\\ \dos_{\rm s}\pars{\omega} = \Theta\pars{\omega}\,{\Omega \over 2\pi^{2}s^{3}}\,\omega^{2} \\ \mbox{}\\ \hline \end{array} \label{DmsBB} \end{equation}
- $\large\ds{\omega_{\vec{k}} \equiv {k^{2} \over 2m^{*}}\,,\
m^{*} > 0}$. Este modelo describe, por ejemplo, un gas de
partículas bosónicas con Masa
Efectiva
$m^{*}$. \begin{align*} \dos_{\rm m^{*}}\pars{\omega} & = \sum_{\vec{k}}\delta\pars{\omega - {k^{2} \over 2m^{*}}} \\[3mm] & = {\Omega \over \pars{2\pi}^{3}} \int_{0}^{\infty}\bracks{% {\delta\pars{k + \raiz{2m^{*}\omega}} \over k/m^{*}} + {\delta\pars{k - \raiz{2m^{*}\omega}} \over k/m^{*}}}4\pi k^{2}\,\dd k \end{align*} \begin{equation} \begin{array}{|c|} \hline\\ \mbox{}\\ \dos_{\rm m^{*}}\pars{\omega} = \Theta\pars{\omega}\,{\Omega\,{m^{*}}^{3/2} \over \raiz{2}\pi^{2}} \,\omega^{1/2} \\ \mbox{}\\ \hline \end{array} \label{DmstarBB} \end{equation}
En la continuación del presente ejemplo consideraremos situaciones donde $\angles{a\+ b_{\vec{k}}}_{{\cal V}\ =\ 0} = 0$. En tal caso, ${\cal P}\pars{t}$ se reduce a $\pars{~\mbox{ver Ec.}\ \eqref{solgenFkoopBB}~}$
\begin{align*} {\cal P}\pars{t} & = {2\varepsilon \over \hbar}\,{\cal V}\,\Re\sum_{\vec{k}} \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} \\[3mm] & {-{\cal V}\sum_{\vec{q}}\bracks{% -\pars{2\pi}^{2}\ic \angles{b_{\vec{q}}\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}} _{{\cal V}\ =\ 0} \expo{\ic\pars{\omega_{\vec{k}} - \omega_{\vec{q}}}t_{0}} \delta\pars{\omega + \omega_{\vec{q}}} \delta\pars{\omega' + \omega_{\vec{k}}}} \over \omega + \varepsilon - \ic\pi{\cal V}^{2}\dos_{\rm B}\pars{-\omega}}\, \times \\[3mm] & \phantom{\mbox{}=\mbox{}} \expo{-\ic\pars{\omega - \omega'}t} \,{\dd\omega\,\dd\omega' \over \pars{2\pi}^{2}} \end{align*}
\begin{align}
{\cal P}\pars{t} & =
{2\varepsilon \over \hbar}\,{\cal V}^{2}\,\Im\sum_{\vec{k}\vec{q}}
\angles{b_{\vec{q}}\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}
_{{\cal V}\ =\ 0}\,
{\expo{\ic\pars{\omega_{\vec{q}} - \omega_{\vec{k}}}\pars{t - t_{0}}}
\over
\omega_{\vec{q}} - \varepsilon + \ic\Gamma\pars{\omega_{\vec{q}}}}
\label{Ptfinal0BB}
\\[3mm]
\Gamma\pars{\omega} & \equiv
\pi{\cal V}^{2}\dos_{\rm B}\pars{\omega}
\end{align}
Con las expresiones \eqref{DmsBB} y \eqref{DmstarBB}:
\begin{align}
\Gamma_{\rm s}\pars{\omega} & \equiv
\pi{\cal V}^{2}\dos_{\rm s}\pars{\omega} = \alpha_{\rm s}\omega^{2}
\,,\qquad
\alpha_{\rm s} \equiv \Omega\,{{\cal V}^{2} \over 2\pi s^{3}}
\label{gammasBB}
\\[3mm]
\Gamma_{\rm m^{*}}\pars{\omega} & \equiv
\pi{\cal V}^{2}\dos_{\rm m^{*}}\pars{\omega} =
\alpha_{\rm m^{*}}\omega^{1/2}
\,,\qquad
\alpha_{\rm m^{*}} \equiv
\Omega\,{{\cal V}^{2}{m^{*}}^{3/2} \over \raiz{2}\pi}
\label{gammamstarBB}
\end{align}
Algunos Casos Particulares
- $\ds{\angles{b_{\vec{q}}\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}
_{{\cal V}\ =\ 0} =
\delta_{\vec{q}\vec{k}}\delta_{\vec{k}\vec{p}}}$: Esta
condición inicial describe la presencia de un solo
bosón del reservorio con momentum $\vec{p}$ $\pars{~\mbox{en
el instante inicial}\ t_{0}~}$.
La expresión \eqref{Ptfinal0BB} se reduce a
\begin{equation} {\cal P}\pars{t} = {\varepsilon \over h}\,{\cal V}^{2}\, {\Gamma\pars{\omega_{\vec{p}}}/\pi \over \pars{\omega_{\vec{p}} - \varepsilon}^{2} + \Gamma^{2}\pars{\omega_{\vec{p}}}} \label{someparticularPBB} \end{equation}- Con el modelo $\dos_{\rm s}\pars{\omega}$ que conduce a
\eqref{gammasBB} $\pars{~\mbox{ver}\ \eqref{someparticularPBB}~}$:
\begin{equation}
{\cal P}_{\rm s}\pars{t} =
{\varepsilon \over h}\,{\cal V}^{2}\,
{\alpha_{\rm s}\omega_{\vec{p}}^{2}/\pi
\over
\pars{\omega_{\vec{p}} - \varepsilon}^{2} +
\alpha_{\rm s}^{2}\omega_{\vec{p}}^{4}}
\end{equation}
${\cal P}_{\rm s}\pars{t}\ \mbox{vs.}\ \omega_{\vec{p}}$
$\pars{~\mbox{en unidades adimensionales con}\ \varepsilon = 1~}$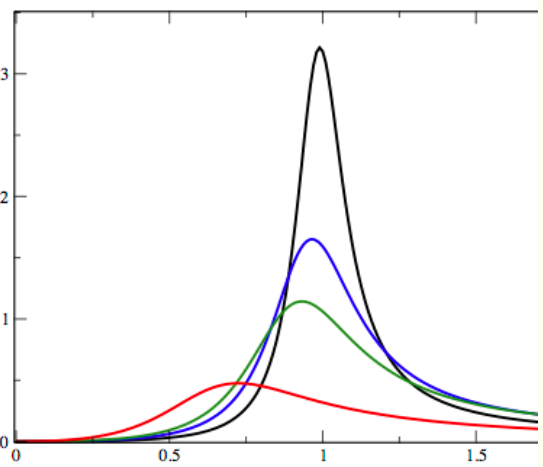
$\omega_{\vec{p}}$
Para valores pequeños de $\alpha_{\rm s}$ ( linea $\color{#000}{negra}$ ) la absorción de energía ocurre para valores cercanos a $\varepsilon = 1$ $\pars{~\omega_{\vec{p}} \approx \varepsilon~}$. A medida que $\alpha_{\rm s}$ se incrementa ( lineas $\color{#00f}{azul}$, $\color{darkgreen}{verde}$ y $\color{#f00}{roja}$ ), la absorción ocurre para valores de la energía que se desplazan
hacía valores menores de $\omega_{\vec{p}}$ mientras laaltura
de la máxima absorción disminuye. - Con el modelo $\dos_{\rm m^{*}}\pars{\omega}$ que conduce a
\eqref{gammamstarBB} $\pars{~\mbox{ver}\
\eqref{someparticularPBB}~}$:
\begin{equation}
{\cal P}_{\rm m^{*}}\pars{t} =
{\varepsilon \over h}\,{\cal V}^{2}\,
{\alpha_{\rm m^{*}}\omega_{\vec{p}}^{1/2}/\pi
\over
\pars{\omega_{\vec{p}} - \varepsilon}^{2} +
\alpha_{\rm m^{*}}^{2}\omega_{\vec{p}}}
\end{equation}
${\cal P}_{\rm m^{*}}\pars{t}\ \mbox{vs.}\ \omega_{\vec{p}}$
$\pars{~\mbox{en unidades adimensionales con}\ \varepsilon = 1~}$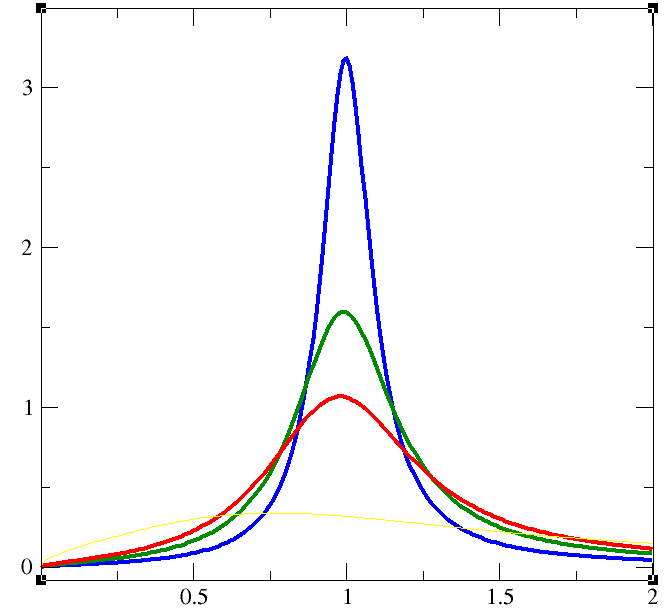
$\omega_{\vec{p}}$
Para valores pequeños de $\alpha_{\rm m^{*}}$ ( linea $\color{#00f}{azul}$ y $\color{darkgreen}{verde}$, por ejemplo ) la absorción de energía ocurre para valores cercanos a $\varepsilon = 1$ $\pars{~\omega_{\vec{p}} \approx \varepsilon~}$. A medida que $\alpha_{\rm m^{*}}$ se incrementa ( linea $\color{#f00}{roja}$ ), la absorción ocurre para valores de la energía que se desplazan
hacía valores menores de $\omega_{\vec{p}}$ ( pero permanececercano
a $\varepsilon$ ) mientras laaltura
de la máxima absorción disminuye.
- Con el modelo $\dos_{\rm s}\pars{\omega}$ que conduce a
\eqref{gammasBB} $\pars{~\mbox{ver}\ \eqref{someparticularPBB}~}$:
\begin{equation}
{\cal P}_{\rm s}\pars{t} =
{\varepsilon \over h}\,{\cal V}^{2}\,
{\alpha_{\rm s}\omega_{\vec{p}}^{2}/\pi
\over
\pars{\omega_{\vec{p}} - \varepsilon}^{2} +
\alpha_{\rm s}^{2}\omega_{\vec{p}}^{4}}
\end{equation}
- $\ds{\angles{b_{\vec{q}}\+\pars{t_{0}}b_{\vec{k}}\pars{t_{0}}}
_{{\cal V}\ =\ 0} =
{\delta_{\vec{q}\vec{k}} \over
\expo{\beta\omega_{\vec{k}}} - 1}}$: Esta
condición inicial corresponde a equilibrio
termodinámico, a temperatura $T$
$\ds{\pars{~\beta \equiv {1 \over \kb T}~}}$, del reservorio de
bosones en el instante inicial $t_{0}$.
$\bose_{\rm B}\pars{\omega} \equiv \pars{\expo{\beta\omega} - 1}^{-1}$
es la Función de Distribución de Bose-Einstein.
\eqref{Ptfinal0BB} se reduce a
\begin{align*} {\cal P}\pars{t} & = {2\varepsilon \over \hbar}\,{\cal V}^{2}\,\Im\sum_{\vec{k}} {1 \over \omega_{\vec{k}} - \varepsilon + \ic\Gamma\pars{\omega_{\vec{k}}}}\, \bose_{\rm B}\pars{\omega_{\vec{k}}} \\[3mm] & = {2\varepsilon \over \hbar}\,{\cal V}^{2}\,\Im\int_{0}^{\infty} {\dos_{\rm B}\pars{\omega} \over \omega - \varepsilon + \ic\Gamma\pars{\omega}}\, \bose_{\rm B}\pars{\omega}\,\dd\omega \end{align*} tal que $\pars{~\mbox{ver}\ \eqref{DmsBB}\ \mbox{y}\ \eqref{DmstarBB}~}$- $\ds{{\cal P}_{\rm s}\pars{t} = {2\varepsilon \over \pi hs^{3}}\,\Omega{\cal V}^{2}\, \Im\int_{0}^{\infty} {\omega^{2} \over \omega - \varepsilon + \ic\alpha_{\rm s}\omega^{2}}\, \bose_{\rm B}\pars{\omega}\,\dd\omega}$
- $\ds{{\cal P}_{\rm m^{*}}\pars{t} = {2\raiz{2}\varepsilon{m^{*}}^{3/2} \over \pi h}\, \Omega{\cal V}^{2}\,\Im\int_{0}^{\infty} {\omega^{1/2} \over \omega - \varepsilon + \ic\alpha_{\rm m^{*}}\omega^{1/2}}\, \bose_{\rm B}\pars{\omega}\,\dd\omega}$
Note que $\pars{~\mbox{con}\ \kb = 1~}$
\begin{align} {\cal P}_{\rm s}\pars{t} & = -\,{2\varepsilon \over \pi hs^{3}}\,\Omega{\cal V}^{2}\, \Re\braces{T^{3}\int_{0}^{\infty}\expo{-x}\bracks{ {x \over T\pars{\alpha_{\rm s}Tx - \ic}x + \varepsilon\ic}\, {x \over 1 - \expo{-x}}}\dd x} \end{align} la cual es una expresión adecuada para realizar una integración numérica mediante el uso de la Cuadratura de Gauss-Laguerrea $10$ puntos
. El resultado se muestra gráficamente a continuación:$\ds{\Re\braces{T^{3}\int_{0}^{\infty}\expo{-x}\bracks{ {x \over T\pars{\alpha_{\rm s}Tx - \ic}x + \varepsilon\ic}\, {x \over 1 - \expo{-x}}}\dd x}}$
$\pars{~\mbox{en unidades adimensionales}. T = 1.\ \alpha_{\rm s} = 0.1~}$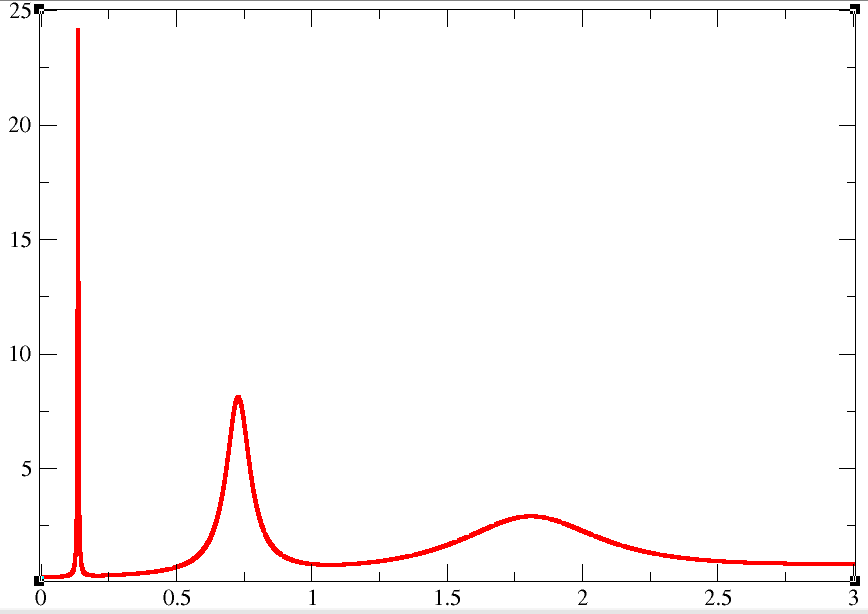
$\varepsilon$
El programa que genera la data
de esta gráfica puede verse en el Apéndice Utilidades.